Limit point of a trajectory
 of a dynamical system
of a dynamical system 
A point
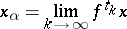 | (1) |
(an  -limit point) or
-limit point) or
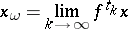 | (2) |
(an  -limit point), where
-limit point), where  is a sequence such that
is a sequence such that 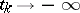 as
as  in (1), or
in (1), or  as
as  in (2), and for which the limits in (1) or (2) exist.
in (2), and for which the limits in (1) or (2) exist.
For a trajectory 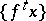 of a dynamical system
of a dynamical system  (or, in other words, for
(or, in other words, for  , cf. [1]), an
, cf. [1]), an 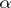 -limit point (
-limit point (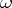 -limit point) is the same as an
-limit point) is the same as an 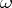 -limit point (
-limit point ( -limit point) of the trajectory
-limit point) of the trajectory  of the dynamical system
of the dynamical system  (the system with reverse time). The set
(the system with reverse time). The set 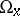 (
(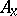 ) of all
) of all 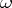 -limit points (
-limit points (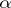 -limit points) of a trajectory
-limit points) of a trajectory 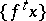 is called the
is called the 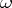 -limit set (
-limit set (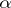 -limit set) of this trajectory (cf. Limit set of a trajectory).
-limit set) of this trajectory (cf. Limit set of a trajectory).
References
| [1] | V.V. Nemytskii, V.V. Stepanov, "Qualitative theory of differential equations" , Princeton Univ. Press (1960) (Translated from Russian) |
Comments
For a dynamical system with discrete time (or, a cascade) similar definitions and the same terminology are used (now in the above the sequences 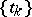 have to be in
have to be in 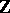 ).
).
Limit point of a trajectory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Limit_point_of_a_trajectory&oldid=17356