Limit-absorption principle
A manner for uniquely finding solutions to equations analogous to the Helmholtz equation by introducing an infinitesimal absorption. Mathematically the principle is as follows. Let  be an unbounded region in
be an unbounded region in 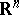 , let
, let 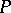 be the self-adjoint operator on
be the self-adjoint operator on 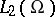 given by the differential expression
given by the differential expression 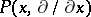 ,
, 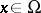 , and homogeneous boundary conditions on
, and homogeneous boundary conditions on  and let
and let 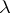 be a point in the continuous spectrum of
be a point in the continuous spectrum of 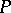 . Then for
. Then for 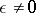 the equation
the equation
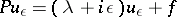 |
is uniquely solvable in 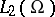 , and in certain cases it is possible to find solutions
, and in certain cases it is possible to find solutions 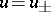 of the equation
of the equation
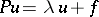 |
by the limit transition
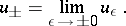 |
It is assumed here that 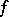 has compact support and the convergence
has compact support and the convergence 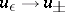 , as
, as 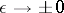 , is understood in the sense of
, is understood in the sense of 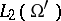 , where
, where 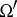 is an arbitrary bounded set in
is an arbitrary bounded set in  . Since
. Since 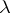 is a point of the continuous spectrum of
is a point of the continuous spectrum of 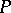 , the limit in
, the limit in 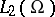 does not exist, in general.
does not exist, in general.
The first limit-absorption principle was formulated for the Helmholtz equation in 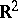 (cf. [1]):
(cf. [1]):
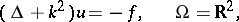 |
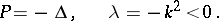 |
The solutions 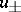 found using this principle are diverging or converging waves and satisfy the radiation conditions at infinity. These results were carried over (cf. [2], [3]) to elliptic boundary value problems in the exterior of bounded regions in
found using this principle are diverging or converging waves and satisfy the radiation conditions at infinity. These results were carried over (cf. [2], [3]) to elliptic boundary value problems in the exterior of bounded regions in 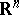 for an operator
for an operator
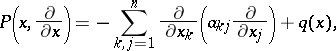 | (*) |
where the coefficients 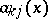 tend to constants sufficiently rapidly as
tend to constants sufficiently rapidly as 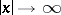 . In order that the limit-absorption principle holds in this case it is necessary that
. In order that the limit-absorption principle holds in this case it is necessary that 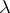 is not an eigen value of
is not an eigen value of 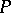 or that
or that 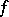 is orthogonal to the eigen functions. A theorem of T. Kato (cf. [3]) gives sufficient conditions for the absence of eigen values in the continuous spectrum of the operator
is orthogonal to the eigen functions. A theorem of T. Kato (cf. [3]) gives sufficient conditions for the absence of eigen values in the continuous spectrum of the operator 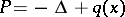 . Such a theorem has been obtained for the operator (*) (cf. [3]). The limit-absorption principle has been substantiated for certain regions with non-compact boundary (cf. [3], [4]).
. Such a theorem has been obtained for the operator (*) (cf. [3]). The limit-absorption principle has been substantiated for certain regions with non-compact boundary (cf. [3], [4]).
A limit-absorption principle and corresponding radiation conditions have been found for higher-order equations and for systems of equations (cf. [5]–[7]); they consist of the following. Let 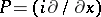 be an elliptic (or hypo-elliptic) operator satisfying: 1) the polynomial
be an elliptic (or hypo-elliptic) operator satisfying: 1) the polynomial 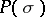 has real coefficients; 2) the surface
has real coefficients; 2) the surface 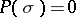 ,
, 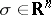 , decomposes into connected smooth surfaces
, decomposes into connected smooth surfaces 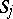 ,
, 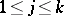 , whose curvatures do not vanish; and 3)
, whose curvatures do not vanish; and 3) 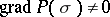 on
on 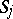 . Suppose that an orientation is given on
. Suppose that an orientation is given on 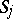 , i.e. for each surface one has independently chosen a normal direction
, i.e. for each surface one has independently chosen a normal direction  . Let
. Let 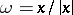 , let
, let 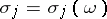 be a point on
be a point on 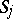 at which
at which  and
and 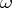 have identical direction and let
have identical direction and let 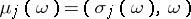 . Then the function
. Then the function 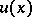 does satisfy the radiation conditions if it can be represented as
does satisfy the radiation conditions if it can be represented as
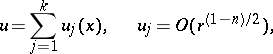 |
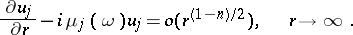 |
These conditions determine a unique solution of the equation
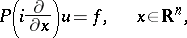 |
for any function 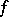 with compact support. The limit-absorption principle for this equation is that this solution can be obtained as the limit, for
with compact support. The limit-absorption principle for this equation is that this solution can be obtained as the limit, for 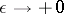 , of the unique solution
, of the unique solution 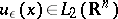 of the elliptic equation
of the elliptic equation
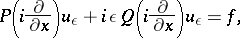 |
where 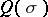 has real coefficients and
has real coefficients and 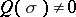 on
on 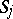 . Depending on the choice of
. Depending on the choice of 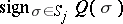 ,
, 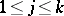 , one obtains in the limit solutions satisfying the radiation conditions corresponding to some orientation of
, one obtains in the limit solutions satisfying the radiation conditions corresponding to some orientation of 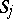 . This principle has been substantiated for higher-order equations and systems with variable coefficients in the exterior of bounded regions (cf. [5]–[7]), as well as in the case of non-convex
. This principle has been substantiated for higher-order equations and systems with variable coefficients in the exterior of bounded regions (cf. [5]–[7]), as well as in the case of non-convex  . For such equations there is also a uniqueness theorem of Kato type.
. For such equations there is also a uniqueness theorem of Kato type.
References
| [1] | W. [V.S. Ignatovskii] Ignatowsky, "Reflexion elektromagnetischer Wellen an einem Drahte" Ann. der Physik , 18 : 13 (1905) pp. 495–522 |
| [2] | A.Ya. Povzner, "On the decomposition of arbitrary functions into eigenfunctions of the operator 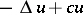 " Mat. Sb. , 32 : 1 (1953) pp. 109–156 (In Russian) " Mat. Sb. , 32 : 1 (1953) pp. 109–156 (In Russian) |
| [3] | D.M. Eidus, "The principle of limiting amplitude" Russian Math. Surveys , 24 : 3 (1969) pp. 97–167 Uspekhi Mat. Nauk , 24 : 3 (1969) pp. 91–156 |
| [4] | A.V. Sveshnikov, "The limit absorption principle for a wave guide" Dokl. Akad. Nauk SSSR , 80 : 3 (1951) pp. 345–347 (In Russian) |
| [5] | B.R. Vainberg, "Principles of radiation, limit absorption and limit amplitude in the general theory of partial differential equations" Russian Math. Surveys , 21 : 3 (1966) pp. 115–193 Uspekhi Mat. Nauk , 21 : 3 (1966) pp. 115–194 |
| [6] | B.R. Vainberg, "On elliptic problems in unbounded domains" Math. USSR Sb. , 4 (1968) pp. 419–444 Mat. Sb. , 75 : 3 (1968) pp. 454–480 |
| [7] | B.R. Vainberg, "Asymptotic methods in equations of mathematical physics" , Gordon & Breach (1988) (Translated from Russian) |
Limit-absorption principle. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Limit-absorption_principle&oldid=13580