Lie group, supersolvable
triangular Lie group
A connected real Lie group  for which the eigen values of the operators
for which the eigen values of the operators  of adjoint representation (cf. Adjoint representation of a Lie group) are real for any element
of adjoint representation (cf. Adjoint representation of a Lie group) are real for any element  .
.
A connected Lie group  is supersolvable if and only if its Lie algebra
is supersolvable if and only if its Lie algebra  is supersolvable, so a number of properties of the class of supersolvable Lie groups are parallel with properties of supersolvable Lie algebras (cf. Lie algebra, supersolvable).
is supersolvable, so a number of properties of the class of supersolvable Lie groups are parallel with properties of supersolvable Lie algebras (cf. Lie algebra, supersolvable).
The following fixed-point theorem is true for a supersolvable Lie group [2]: Any supersolvable Lie subgroup  of a projective group has a fixed point in every
of a projective group has a fixed point in every  -invariant closed subset of the real projective space. There are also other analogues of properties of complex solvable Lie groups. An arbitrary connected Lie group
-invariant closed subset of the real projective space. There are also other analogues of properties of complex solvable Lie groups. An arbitrary connected Lie group  has maximal connected supersolvable Lie groups
has maximal connected supersolvable Lie groups  , and they are all conjugate in
, and they are all conjugate in 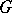 (see [2]). To study the structure of real semi-simple Lie groups, the subgroup
(see [2]). To study the structure of real semi-simple Lie groups, the subgroup 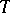 is often used as the real analogue of a Borel subgroup.
is often used as the real analogue of a Borel subgroup.
A simply-connected supersolvable Lie group can be isomorphically imbedded in the group of real upper-triangular matrices over 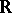 with positive diagonal elements (which is itself supersolvable).
with positive diagonal elements (which is itself supersolvable).
References
| [1] | A. Borel, "Linear algebraic groups" , Benjamin (1969) |
| [2] | E.B. Vinberg, "The Morozov–Borel theorem for real Lie groups" Soviet Math. Dokl. , 2 (1961) pp. 1416–1419 Dokl. Akad. Nauk SSSR , 141 (1961) pp. 270–273 |
Comments
In [1] the phrase "trigonalizable Lie grouptrigonalizable Lie group" is used instead of supersolvable. The literal translation of the Russian expression is fully-solvable Lie group.
Lie group, supersolvable. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lie_group,_supersolvable&oldid=15494