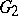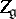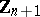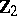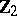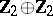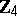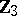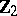Difference between revisions of "Lie group, semi-simple"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 26: | Line 26: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> J.F. Adams, "Lectures on Lie groups" , Benjamin (1969) {{MR|0252560}} {{ZBL|0206.31604}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> J.-P. Serre, "Lie algebras and Lie groups" , Benjamin (1965) (Translated from French) {{MR|0218496}} {{ZBL|0132.27803}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> A.I. Sirota, A.S. Solodovnikov, "Noncompact semisimple Lie groups" ''Russian Math. Surveys'' , '''18''' : 3 (1963) pp. 85–140 ''Uspekhi Mat. Nauk'' , '''18''' : 3 (1963) pp. 87–144 {{MR|155929}} {{ZBL|0132.02101}} </TD></TR></table> |
| Line 36: | Line 36: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> Harish-Chandra, "Collected works" , '''1–4''' , Springer (1984) {{MR|}} {{ZBL|0699.62084}} {{ZBL|0653.01018}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> R.W. Carter, "Finite groups of Lie type: Conjugacy classes and complex characters" , Wiley (Interscience) (1985)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> J.A. Wolf, "Spaces of constant curvature" , Publish or Perish (1974) {{MR|0343214}} {{ZBL|0281.53034}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> G. Hochschild, "The structure of Lie groups" , Holden-Day (1965) {{MR|0207883}} {{ZBL|0131.02702}} </TD></TR></table> |
Revision as of 14:50, 24 March 2012
A connected Lie group that does not contain non-trivial connected solvable (or, equivalently, connected Abelian) normal subgroups. A connected Lie group is semi-simple if and only if its Lie algebra is semi-simple (cf. Lie algebra, semi-simple). A connected Lie group 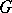 is said to be simple if its Lie algebra is simple, that is, if
is said to be simple if its Lie algebra is simple, that is, if 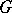 does not contain non-trivial connected normal subgroups other than
does not contain non-trivial connected normal subgroups other than 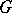 . A connected Lie group is semi-simple if and only if it splits into a locally direct product of simple non-Abelian normal subgroups.
. A connected Lie group is semi-simple if and only if it splits into a locally direct product of simple non-Abelian normal subgroups.
The classification of semi-simple Lie groups reduces to the local classification, that is, to the classification of semi-simple Lie algebras (cf. Lie algebra, semi-simple), and also to the global classification of the Lie groups 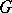 that correspond to a given semi-simple Lie algebra
that correspond to a given semi-simple Lie algebra 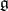 .
.
In the case of Lie groups over the field 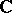 of complex numbers the main result of the local classification is that every simply-connected simple non-Abelian complex Lie group is isomorphic to one of the groups
of complex numbers the main result of the local classification is that every simply-connected simple non-Abelian complex Lie group is isomorphic to one of the groups 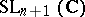 ,
, 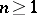 ,
, 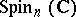 ,
, 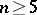 (the universal covering of the group
(the universal covering of the group 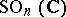 ),
), 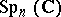 ,
, 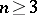 (see Classical group), or one of the exceptional complex Lie groups (see Lie algebra, exceptional). The global classification of the Lie groups corresponding to a semi-simple Lie algebra
(see Classical group), or one of the exceptional complex Lie groups (see Lie algebra, exceptional). The global classification of the Lie groups corresponding to a semi-simple Lie algebra 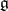 over
over 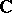 goes as follows. Let
goes as follows. Let 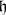 be a Cartan subalgebra of
be a Cartan subalgebra of 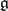 and let
and let 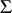 be the root system of
be the root system of 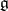 with respect to
with respect to 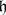 . To every semi-simple Lie group
. To every semi-simple Lie group 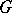 with Lie algebra
with Lie algebra 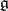 corresponds a lattice
corresponds a lattice 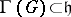 that is the kernel of the exponential mapping
that is the kernel of the exponential mapping 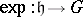 . In particular, if
. In particular, if 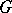 is simply connected, then
is simply connected, then 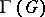 coincides with the lattice
coincides with the lattice 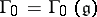 generated by the elements
generated by the elements 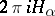 ,
, 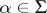 (see Lie algebra, semi-simple), and if
(see Lie algebra, semi-simple), and if 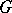 is a group without centre (an adjoint group), then
is a group without centre (an adjoint group), then 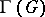 is the lattice
is the lattice
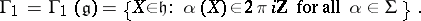 |
In the general case 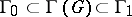 . For any additive subgroup
. For any additive subgroup 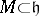 satisfying the condition
satisfying the condition 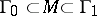 there is a unique (up to isomorphism) connected Lie group
there is a unique (up to isomorphism) connected Lie group 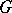 with Lie algebra
with Lie algebra 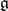 such that
such that 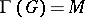 . The centre of
. The centre of 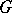 is isomorphic to
is isomorphic to 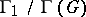 , and for the fundamental group one has:
, and for the fundamental group one has:
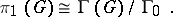 |
The quotient group 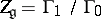 (the centre of the simply-connected Lie group with Lie algebra
(the centre of the simply-connected Lie group with Lie algebra 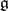 ) is finite and for the different types of simple Lie algebras
) is finite and for the different types of simple Lie algebras 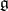 it has the following form:'
it has the following form:'
<tbody> </tbody>
|
The order of the group 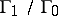 is the same as the number of vertices with coefficient 1 in the extended Dynkin diagram of
is the same as the number of vertices with coefficient 1 in the extended Dynkin diagram of 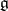 ; discarding one of the vertices gives the Dynkin diagram. A similar classification holds for compact real semi-simple Lie groups, each of which is imbedded in a unique complex semi-simple Lie group as a maximal compact subgroup (see Lie group, compact).
; discarding one of the vertices gives the Dynkin diagram. A similar classification holds for compact real semi-simple Lie groups, each of which is imbedded in a unique complex semi-simple Lie group as a maximal compact subgroup (see Lie group, compact).
The global classification of non-compact real semi-simple Lie groups can be carried out in a similar but more complicated way. In particular, the centre 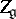 of the simply-connected Lie group corresponding to a semi-simple Lie algebra
of the simply-connected Lie group corresponding to a semi-simple Lie algebra 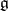 over
over 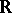 can be calculated as follows. Let
can be calculated as follows. Let 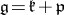 be the Cartan decomposition, where
be the Cartan decomposition, where 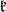 is a maximal compact subalgebra of
is a maximal compact subalgebra of 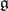 and
and 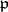 is its orthogonal complement with respect to the Killing form, let
is its orthogonal complement with respect to the Killing form, let 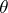 be the corresponding involutive automorphism, extended to
be the corresponding involutive automorphism, extended to 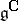 ,
, 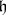 the Cartan subalgebra of
the Cartan subalgebra of 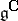 containing a Cartan subalgebra
containing a Cartan subalgebra 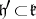 ,
, 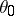 an automorphism of
an automorphism of 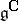 that coincides with
that coincides with 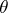 on the roots with respect to
on the roots with respect to 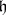 and extended to the root vectors in an appropriate way, and
and extended to the root vectors in an appropriate way, and 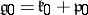 the Cartan decomposition of the real form
the Cartan decomposition of the real form 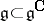 corresponding to
corresponding to 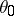 . Then
. Then 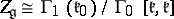 (see [3], where this group is calculated for all types of simple algebras
(see [3], where this group is calculated for all types of simple algebras 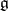 over
over 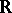 ).
).
Every complex semi-simple Lie group 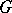 has the unique structure of an affine algebraic group compatible with the analytic structure specified on it, and any analytic homomorphism of
has the unique structure of an affine algebraic group compatible with the analytic structure specified on it, and any analytic homomorphism of 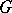 to an algebraic group is rational. The corresponding algebra of regular functions on
to an algebraic group is rational. The corresponding algebra of regular functions on 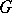 coincides with the algebra of holomorphic representation functions. On the other hand, a non-compact real semi-simple Lie group does not always admit a faithful linear representation — the simplest example is the simply-connected Lie group corresponding to the Lie algebra
coincides with the algebra of holomorphic representation functions. On the other hand, a non-compact real semi-simple Lie group does not always admit a faithful linear representation — the simplest example is the simply-connected Lie group corresponding to the Lie algebra 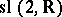 . If
. If 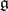 is a semi-simple Lie algebra over
is a semi-simple Lie algebra over 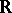 , then in the centre
, then in the centre 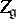 of the simply-connected group
of the simply-connected group 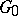 corresponding to
corresponding to 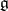 there is a smallest subgroup
there is a smallest subgroup 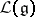 , called the linearizer, such that
, called the linearizer, such that 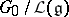 is isomorphic to a linear semi-simple Lie group. If
is isomorphic to a linear semi-simple Lie group. If 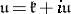 is the compact real form of
is the compact real form of 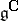 , then
, then
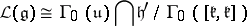 |
(see [3], where this group is calculated for all types of simple Lie algebras 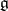 ).
).
References
| [1] | J.F. Adams, "Lectures on Lie groups" , Benjamin (1969) MR0252560 Zbl 0206.31604 |
| [2] | J.-P. Serre, "Lie algebras and Lie groups" , Benjamin (1965) (Translated from French) MR0218496 Zbl 0132.27803 |
| [3] | A.I. Sirota, A.S. Solodovnikov, "Noncompact semisimple Lie groups" Russian Math. Surveys , 18 : 3 (1963) pp. 85–140 Uspekhi Mat. Nauk , 18 : 3 (1963) pp. 87–144 MR155929 Zbl 0132.02101 |
Comments
The (infinite-dimensional) representation theory of semi-simple Lie groups over 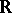 has been created for a large part by Harish-Chandra. See also the excellent survey of Harish-Chandra's work by V.S. Varadarajan in the collected works [a1].
has been created for a large part by Harish-Chandra. See also the excellent survey of Harish-Chandra's work by V.S. Varadarajan in the collected works [a1].
The 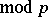 reductions of semi-simple Lie groups over
reductions of semi-simple Lie groups over 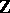 are called the Chevalley groups (cf. Chevalley group), and from them most of the finite simple groups can be obtained (with the exception of the alternating group and the 26 sporadic groups, cf. Sporadic simple group). For a survey of the structure and representation theory of the Chevalley groups see [a2].
are called the Chevalley groups (cf. Chevalley group), and from them most of the finite simple groups can be obtained (with the exception of the alternating group and the 26 sporadic groups, cf. Sporadic simple group). For a survey of the structure and representation theory of the Chevalley groups see [a2].
References
| [a1] | Harish-Chandra, "Collected works" , 1–4 , Springer (1984) Zbl 0699.62084 Zbl 0653.01018 |
| [a2] | R.W. Carter, "Finite groups of Lie type: Conjugacy classes and complex characters" , Wiley (Interscience) (1985) |
| [a3] | J.A. Wolf, "Spaces of constant curvature" , Publish or Perish (1974) MR0343214 Zbl 0281.53034 |
| [a4] | G. Hochschild, "The structure of Lie groups" , Holden-Day (1965) MR0207883 Zbl 0131.02702 |
Lie group, semi-simple. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lie_group,_semi-simple&oldid=18993
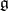
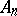
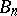
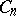
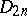
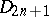
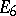
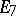
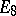 ,
, 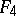 ,
,