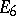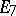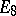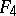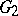Lie algebra, semi-simple
A Lie algebra that has no non-zero solvable ideals (see Lie algebra, solvable). Henceforth finite-dimensional semi-simple Lie algebras over a field 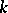 of characteristic 0 are considered (for semi-simple Lie algebras over a field of non-zero characteristic see Lie algebra).
of characteristic 0 are considered (for semi-simple Lie algebras over a field of non-zero characteristic see Lie algebra).
The fact that a finite-dimensional Lie algebra 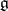 is semi-simple is equivalent to any of the following conditions:
is semi-simple is equivalent to any of the following conditions:
1) 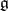 does not contain non-zero Abelian ideals;
does not contain non-zero Abelian ideals;
2) the Killing form of 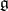 is non-singular (Cartan's criterion);
is non-singular (Cartan's criterion);
3) 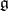 splits into the direct sum of non-Abelian simple ideals;
splits into the direct sum of non-Abelian simple ideals;
4) every finite-dimensional linear representation of 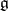 is completely reducible (in other words: every finite-dimensional
is completely reducible (in other words: every finite-dimensional 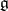 -module is semi-simple);
-module is semi-simple);
5) the one-dimensional cohomology of 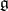 with values in an arbitrary finite-dimensional
with values in an arbitrary finite-dimensional 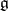 -module is trivial.
-module is trivial.
Any ideal and any quotient algebra of a semi-simple Lie algebra is also semi-simple. The decomposition of a semi-simple Lie algebra mentioned in condition 3) is unique. A special case of condition 5) is the following assertion: All derivations of a semi-simple Lie algebra are inner. The property of a Lie algebra of being semi-simple is preserved by both extensions and restrictions of the ground field.
Let 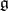 be a semi-simple Lie algebra over an algebraically closed field
be a semi-simple Lie algebra over an algebraically closed field 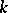 . The adjoint representation maps
. The adjoint representation maps 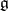 isomorphically onto the linear Lie algebra
isomorphically onto the linear Lie algebra 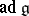 , which is the Lie algebra of the algebraic group
, which is the Lie algebra of the algebraic group 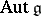 of all automorphisms of
of all automorphisms of 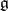 and is therefore an algebraic Lie algebra (cf. Lie algebra, algebraic). An element
and is therefore an algebraic Lie algebra (cf. Lie algebra, algebraic). An element 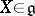 is said to be semi-simple (nilpotent) if
is said to be semi-simple (nilpotent) if  is semi-simple (respectively, nilpotent). This property of an element
is semi-simple (respectively, nilpotent). This property of an element 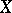 is preserved by any homomorphism of
is preserved by any homomorphism of 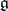 into another semi-simple Lie algebra. The identity component
into another semi-simple Lie algebra. The identity component  coincides with the group of inner automorphisms of
coincides with the group of inner automorphisms of 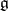 , that is, it is generated by the automorphisms of the form
, that is, it is generated by the automorphisms of the form 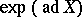 ,
, 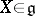 .
.
In the study of semi-simple Lie algebras over an algebraically closed field 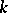 an important role is played by the roots of a semi-simple Lie algebra, which are defined as follows. Let
an important role is played by the roots of a semi-simple Lie algebra, which are defined as follows. Let 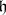 be a Cartan subalgebra of
be a Cartan subalgebra of 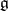 . For a non-zero linear function
. For a non-zero linear function 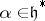 , let
, let 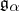 denote the linear subspace of
denote the linear subspace of 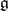 given by the condition
given by the condition
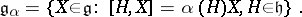 |
If 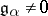 , then
, then 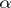 is called a root of
is called a root of 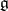 with respect to
with respect to 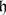 . The set
. The set 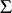 of all non-zero roots is called the root system, or system of roots, of
of all non-zero roots is called the root system, or system of roots, of 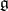 . One has the root decomposition
. One has the root decomposition
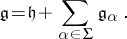 |
The root system and the root decomposition of a semi-simple Lie algebra have the following properties:
a) 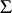 generates
generates 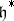 and is a reduced root system in the abstract sense (in the linear hull of
and is a reduced root system in the abstract sense (in the linear hull of 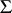 over the field of the real numbers). The system
over the field of the real numbers). The system 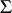 is irreducible if and only if
is irreducible if and only if 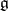 is simple.
is simple.
b) For any 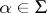 ,
,
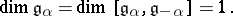 |
There is a unique element 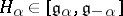 such that
such that 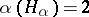 .
.
c) For every non-zero 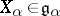 there is a unique
there is a unique 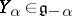 such that
such that 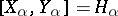 , and
, and
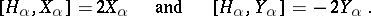 |
Moreover,
 |
where  is the scalar product induced by the Killing form.
is the scalar product induced by the Killing form.
d) If 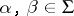 and
and 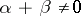 , then
, then 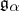 and
and 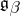 are orthogonal with respect to the Killing form and
are orthogonal with respect to the Killing form and 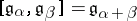 .
.
A basis 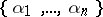 of the root system
of the root system  is also called a system of simple roots of the algebra
is also called a system of simple roots of the algebra 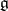 . Let
. Let 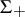 be the system of positive roots with respect to the given basis and let
be the system of positive roots with respect to the given basis and let 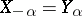
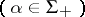 . Then the elements
. Then the elements
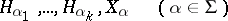 |
form a basis of 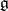 , called a Cartan basis. On the other hand, the elements
, called a Cartan basis. On the other hand, the elements
 |
form a system of generators of 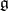 , and the defining relations have the following form:
, and the defining relations have the following form:
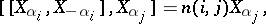 |
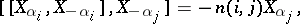 |
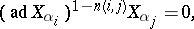 |
 |
Here 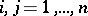 and
and
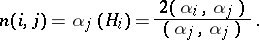 |
Property d) implies that
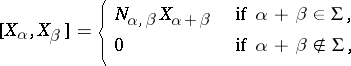 |
where 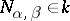 . The elements
. The elements 
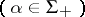 can be chosen in such a way that
can be chosen in such a way that
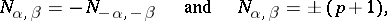 |
where 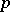 is the largest integer such that
is the largest integer such that 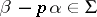 . The corresponding Cartan basis is called a Chevalley basis. The structure constants of
. The corresponding Cartan basis is called a Chevalley basis. The structure constants of 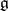 in this basis are integers, which makes it possible to associate with
in this basis are integers, which makes it possible to associate with 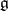 Lie algebras and algebraic groups (see Chevalley group) over fields of arbitrary characteristic. If
Lie algebras and algebraic groups (see Chevalley group) over fields of arbitrary characteristic. If 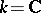 , then the linear hull over
, then the linear hull over 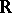 of the vectors
of the vectors
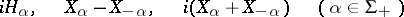 |
is a compact real form of 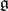 .
.
A semi-simple Lie algebra is defined up to an isomorphism by its Cartan subalgebra and the corresponding root system. More precisely, if 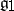 and
and 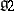 are semi-simple Lie algebras over
are semi-simple Lie algebras over 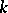 ,
, 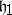 and
and 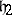 are their Cartan subalgebras and
are their Cartan subalgebras and 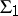 and
and 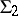 are the corresponding root systems, then every isomorphism
are the corresponding root systems, then every isomorphism 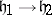 that induces an isomorphism of the root systems
that induces an isomorphism of the root systems 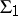 and
and 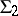 can be extended to an isomorphism
can be extended to an isomorphism 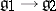 . On the other hand, any reduced root system can be realized as the root system of some semi-simple Lie algebra. Thus, the classification of semi-simple Lie algebras (respectively, simple non-Abelian Lie algebras) over an algebraically closed field
. On the other hand, any reduced root system can be realized as the root system of some semi-simple Lie algebra. Thus, the classification of semi-simple Lie algebras (respectively, simple non-Abelian Lie algebras) over an algebraically closed field 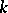 essentially coincides with the classification of reduced root systems (respectively, irreducible reduced root systems).
essentially coincides with the classification of reduced root systems (respectively, irreducible reduced root systems).
Simple Lie algebras that correspond to root systems of types 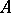 –
–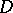 are said to be classical and have the following form.
are said to be classical and have the following form.
Type 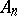 ,
, 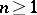 .
. 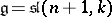 , the algebra of linear transformations of the space
, the algebra of linear transformations of the space 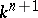 with trace 0;
with trace 0; 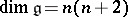 .
.
Type 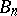 ,
, 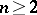 .
.  , the algebra of linear transformations of the space
, the algebra of linear transformations of the space 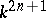 that are skew-symmetric with respect to a given non-singular symmetric bilinear form;
that are skew-symmetric with respect to a given non-singular symmetric bilinear form; 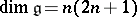 .
.
Type 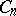 ,
, 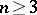 .
. 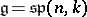 , the algebra of linear transformations of the space
, the algebra of linear transformations of the space 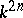 that are skew-symmetric with respect to a given non-singular skew-symmetric bilinear form;
that are skew-symmetric with respect to a given non-singular skew-symmetric bilinear form; 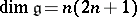 .
.
Type 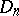 ,
, 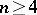 .
. 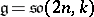 , the algebra of linear transformations of the space
, the algebra of linear transformations of the space  that are skew-symmetric with respect to a given non-singular symmetric bilinear form;
that are skew-symmetric with respect to a given non-singular symmetric bilinear form; 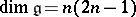 .
.
The simple Lie algebras corresponding to the root systems of types 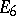 ,
, 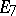 ,
, 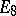 ,
, 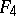 ,
,  are called special, or exceptional (see Lie algebra, exceptional).
are called special, or exceptional (see Lie algebra, exceptional).
The Cartan matrix of a semi-simple Lie algebra over an algebraically closed field also determines this algebra uniquely up to an isomorphism. The Cartan matrices of the simple Lie algebras have the following form:
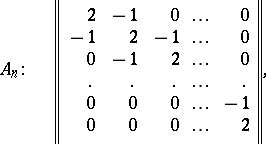 |
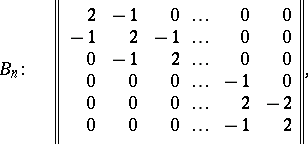 |
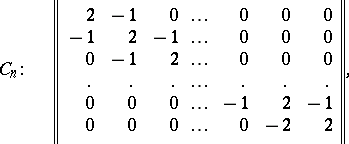 |
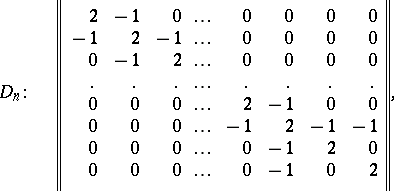 |
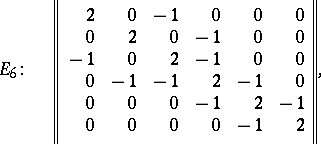 |
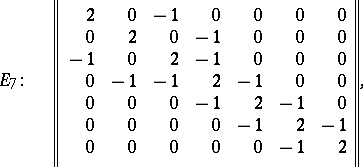 |
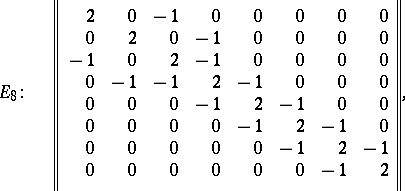 |
 |
The classification of split semi-simple Lie algebras over an arbitrary field 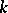 of characteristic zero (a semi-simple Lie algebra
of characteristic zero (a semi-simple Lie algebra 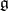 is said to be split if it has a Cartan subalgebra
is said to be split if it has a Cartan subalgebra 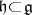 such that all characteristic roots of the operators
such that all characteristic roots of the operators 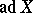 ,
, 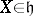 , lie in
, lie in 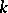 ) goes in the same way as in the case of an algebraically closed field. Namely, to every irreducible reduced root system corresponds a unique split semi-simple Lie algebra. In particular, split semi-simple Lie algebras of types
) goes in the same way as in the case of an algebraically closed field. Namely, to every irreducible reduced root system corresponds a unique split semi-simple Lie algebra. In particular, split semi-simple Lie algebras of types 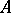 –
–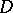 have the form stated above, except that in the cases
have the form stated above, except that in the cases 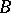 and
and 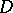 one must consider non-singular symmetric bilinear forms with Witt index
one must consider non-singular symmetric bilinear forms with Witt index  .
.
The problem of classifying arbitrary semi-simple Lie algebras over 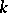 reduces to the following problem: To list, up to an isomorphism, all
reduces to the following problem: To list, up to an isomorphism, all 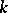 -forms
-forms 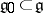 , that is, all
, that is, all 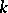 -subalgebras
-subalgebras 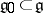 such that
such that 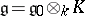 . Here
. Here 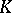 is an algebraically closed extension of
is an algebraically closed extension of 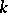 and
and 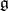 is a given semi-simple Lie algebra over
is a given semi-simple Lie algebra over 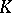 . The solution of this problem can also be obtained in terms of root systems (see Form of an algebraic group; Form of an (algebraic) structure). When
. The solution of this problem can also be obtained in terms of root systems (see Form of an algebraic group; Form of an (algebraic) structure). When 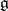 is a classical simple Lie algebra over
is a classical simple Lie algebra over 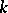 (other than
(other than 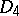 ), there is another method of classifying
), there is another method of classifying 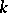 -forms in
-forms in 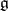 , based on an examination of simple associative algebras (see [3]).
, based on an examination of simple associative algebras (see [3]).
When 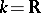 the classification of semi-simple Lie algebras goes as follows (see [6], [7]). Every simple non-Abelian Lie algebra over
the classification of semi-simple Lie algebras goes as follows (see [6], [7]). Every simple non-Abelian Lie algebra over 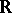 is either a simple Lie algebra over
is either a simple Lie algebra over  (regarded as an algebra over
(regarded as an algebra over 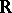 ), or the real form of a simple Lie algebra over
), or the real form of a simple Lie algebra over 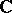 . The classification of real forms
. The classification of real forms 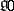 in a simple classical Lie algebra
in a simple classical Lie algebra 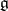 over
over 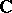 is as follows:
is as follows:
I) Type 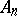 :
: 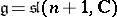 ,
, 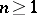 .
.  :
: 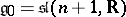 .
. 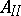 :
: 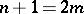 is even,
is even, 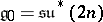 , the subalgebra of elements of
, the subalgebra of elements of 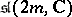 that preserve a certain quaternion structure.
that preserve a certain quaternion structure. 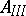 :
: 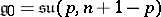 , the subalgebra of elements of
, the subalgebra of elements of 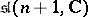 that are skew-symmetric with respect to a non-singular Hermitian form of positive index
that are skew-symmetric with respect to a non-singular Hermitian form of positive index 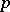 ,
, 
II) Type 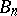 :
: 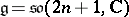 ,
, 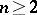 .
. 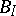 :
: 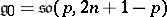 , the algebra of a linear transformations of the space
, the algebra of a linear transformations of the space 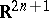 that are skew-symmetric with respect to a non-singular symmetric bilinear form of positive index
that are skew-symmetric with respect to a non-singular symmetric bilinear form of positive index 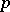 ,
, 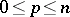 .
.
III) Type 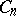 :
: 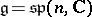 ,
, 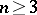 .
. 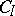 :
: 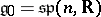 , the algebra of linear transformations of the space
, the algebra of linear transformations of the space 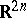 that are skew-symmetric with respect to a non-singular skew-symmetric bilinear form.
that are skew-symmetric with respect to a non-singular skew-symmetric bilinear form. 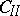 :
: 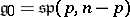 ,
, 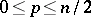 , the subalgebra of
, the subalgebra of 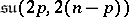 consisting of transformations that preserve a certain quaternion structure.
consisting of transformations that preserve a certain quaternion structure.
IV) Type 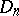 :
: 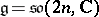 ,
, 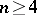 .
. 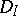 :
: 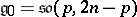 , the algebra of linear transformations of the space
, the algebra of linear transformations of the space 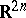 that are skew-symmetric with respect to a non-singular bilinear symmetric form of positive index
that are skew-symmetric with respect to a non-singular bilinear symmetric form of positive index 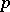 ,
, 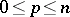 .
. 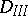 :
: 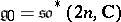 , the subalgebra of
, the subalgebra of 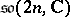 consisting of transformations that preserve a certain quaternion structure.
consisting of transformations that preserve a certain quaternion structure.
Semi-simple Lie algebras over the field 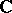 were first considered in papers by W. Killing , who gave a classification of them, although in his proofs there were gaps, which were filled by E. Cartan [2]. In the papers of Killing and Cartan the roots of a Lie algebra appeared as the characteristic roots of the operator
were first considered in papers by W. Killing , who gave a classification of them, although in his proofs there were gaps, which were filled by E. Cartan [2]. In the papers of Killing and Cartan the roots of a Lie algebra appeared as the characteristic roots of the operator 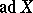 . Cartan also gave a classification of real semi-simple Lie algebras by establishing a deep connection between these algebras and globally symmetric Riemannian spaces (cf. Globally symmetric Riemannian space).
. Cartan also gave a classification of real semi-simple Lie algebras by establishing a deep connection between these algebras and globally symmetric Riemannian spaces (cf. Globally symmetric Riemannian space).
References
| [1a] | W. Killing, "Die Zusammensetzung der stetigen endlichen Transformationsgruppen I" Math. Ann. , 31 (1888) pp. 252–290 |
| [1b] | W. Killing, "Die Zusammensetzung der stetigen endlichen Transformationsgruppen II" Math. Ann. , 33 (1889) pp. 1–48 |
| [1c] | W. Killing, "Die Zusammensetzung der stetigen endlichen Transformationsgruppen III" Math. Ann. , 34 (1889) pp. 57–122 |
| [1d] | W. Killing, "Die Zusammensetzung der stetigen endlichen Transformationsgruppen IV" Math. Ann. , 36 (1890) pp. 161–189 |
| [2] | E. Cartan, "Sur la structure des groupes de transformations finis et continues" , Oeuvres complètes , 1 , Gauthier-Villars (1952) pp. 137–287 |
| [3] | N. Jacobson, "Lie algebras" , Interscience (1962) ((also: Dover, reprint, 1979)) |
| [4] | J.-P. Serre, "Lie algebras and Lie groups" , Benjamin (1965) (Translated from French) |
| [5] | R.G. Steinberg, "Lectures on Chevalley groups" , Yale Univ. Press (1967) |
| [6] | S. Helgason, "Differential geometry, Lie groups, and symmetric spaces" , Acad. Press (1978) |
| [7] | S. Araki, "On root systems and an infinitesimal classification of irreducible symmetric spaces" Osaka J. Math. , 13 (1962) pp. 1–34 |
Comments
The defining relations, mentioned above, 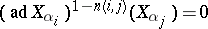 , are known as the Serre relations.
, are known as the Serre relations.
It is customary to encode the information contained in the Cartan matrices 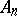 –
–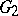 by means of the so-called Dynkin diagrams.'
by means of the so-called Dynkin diagrams.'
<tbody> </tbody>
|
The rules for recovering the Cartan matrix from the corresponding Dynkin diagram (also called Dynkin graph occasionally) are as follows. Number the vertices, e.g.,
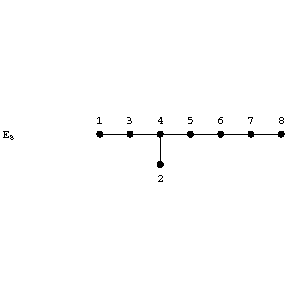
Figure: l058510a
On the diagonal of the Cartan matrix all elements are equal to 2. If nodes 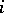 and
and 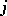 are not directly linked, then the matrix entries
are not directly linked, then the matrix entries 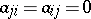 . If two nodes
. If two nodes 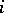 ,
, 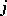 are directly linked by a single edge, then
are directly linked by a single edge, then 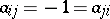 . If two nodes
. If two nodes 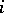 ,
, 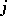 are directly linked by a double, respectively triple, edge and the arrow points from
are directly linked by a double, respectively triple, edge and the arrow points from 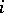 to
to 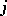 , then
, then 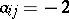 ,
, 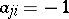 , respectively
, respectively 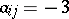 ,
, 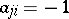 .
.
References
| [a1] | I.B. Frenkel, V.G. Kac, "Basic representations of affine Lie algebras and dual resonance models" Invent. Math. , 62 (1980) pp. 23–66 |
| [a2] | N. Bourbaki, "Elements of mathematics. Lie groups and Lie algebras" , Addison-Wesley (1975) (Translated from French) |
| [a3] | J.-P. Serre, "Algèbres de Lie semi-simples complexes" , Benjamin (1966) |
| [a4] | J.E. Humphreys, "Introduction to Lie algebras and representation theory" , Springer (1972) pp. §5.4 |
Lie algebra, semi-simple. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lie_algebra,_semi-simple&oldid=16829
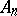
 nodes)
nodes)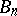
 nodes,
nodes, 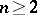 )
)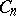
 nodes,
nodes,  )
)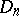
 nodes,
nodes, 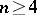 )
)