Lie algebra, exceptional
A simple Lie algebra (see Lie algebra, semi-simple) that is not classical. Over an algebraically closed field of characteristic zero there are 5 exceptional Lie algebras: 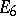 ,
, 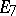 ,
, 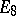 ,
, 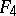 , and
, and 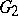 , of dimension 78, 133, 248, 52, and 14, respectively. The indices are the ranks of these Lie algebras. The simplest linear representations of these exceptional Lie algebras have dimensions 27, 56, 248, 26, and 7, respectively. The algebra
, of dimension 78, 133, 248, 52, and 14, respectively. The indices are the ranks of these Lie algebras. The simplest linear representations of these exceptional Lie algebras have dimensions 27, 56, 248, 26, and 7, respectively. The algebra 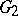 is the algebra of derivations (cf. Derivation in a ring) of the Cayley–Dickson algebra and
is the algebra of derivations (cf. Derivation in a ring) of the Cayley–Dickson algebra and 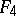 is the algebra of derivations of the unique exceptional Jordan algebra, which can be represented as the algebra of Hermitian matrices of order three over the Cayley–Dickson algebra. The algebra
is the algebra of derivations of the unique exceptional Jordan algebra, which can be represented as the algebra of Hermitian matrices of order three over the Cayley–Dickson algebra. The algebra 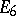 is the linear envelope of the derivations and the multiplications by elements of the exceptional Jordan algebra. The algebras
is the linear envelope of the derivations and the multiplications by elements of the exceptional Jordan algebra. The algebras 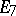 and
and 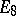 and the forms of all the exceptional Lie algebras over algebraically non-closed fields are also connected with the Cayley–Dickson algebra. The various models of exceptional Lie algebras are obtained by considering their gradings by means of cyclic groups (cf. also Graded algebra). The connected Lie groups corresponding to the exceptional Lie algebras, called exceptional groups, are often denoted by the same letters. For example, the complex group
and the forms of all the exceptional Lie algebras over algebraically non-closed fields are also connected with the Cayley–Dickson algebra. The various models of exceptional Lie algebras are obtained by considering their gradings by means of cyclic groups (cf. also Graded algebra). The connected Lie groups corresponding to the exceptional Lie algebras, called exceptional groups, are often denoted by the same letters. For example, the complex group 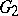 is the group of automorphisms of the Cayley–Dickson algebra over
is the group of automorphisms of the Cayley–Dickson algebra over 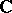 ; the complex group
; the complex group 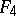 is the group of automorphisms of the exceptional Jordan algebra over
is the group of automorphisms of the exceptional Jordan algebra over 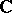 .
.
References
| [1] | N. Jacobson, "Lie algebras" , Interscience (1962) ((also: Dover, reprint, 1979)) MR0148716 MR0143793 Zbl 0121.27504 Zbl 0109.26201 |
| [2] | N. Jacobson, "Exceptional Lie algebras" , M. Dekker (1971) MR0284482 Zbl 0215.38701 |
| [3] | H. Freudenthal, "Oktaven, Ausnahmengruppen und Oktavengeometrie" , Math. Inst. Univ. Utrecht (1960) |
| [4] | B.A. Rozenfel'd, "Einfache Lie-gruppen und nichteuklidische Geometrie" , Algebraical and topological foundations of geometry , Pergamon (1962) pp. 135–155 |
| [5] | E.B. Vinberg, "A construction of the exponential simple Lie algebras" Trudy Sem. Vektor. Tenzor. Anal. , 13 (1966) pp. 7–9 (In Russian) |
| [6] | J. Tits, "Algèbres alternatives, algèbres de Jordan et algèbres de Lie exceptionelles I. Construction" Indag. Mat. , 28 (1966) pp. 233–237 |
| [7] | J. Tits, "Tabellen zu den einfachen Lie Grupppen und ihren Darstellungen" , Lect. notes in math. , 40 , Springer (1967) |
Comments
See Lie algebra, semi-simple for the Cartan matrices and Dynkin diagrams of the exceptional Lie algebras. The same article also contains information on the classification of simple Lie algebras over arbitrary fields, in particular over the real field.
Lie algebra, exceptional. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lie_algebra,_exceptional&oldid=24157