Lie algebra, algebraic
The Lie algebra of an algebraic subgroup (see Algebraic group) of the general linear group of all automorphisms of a finite-dimensional vector space 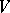 over a field
over a field 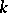 . If
. If 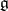 is an arbitrary subalgebra of the Lie algebra of all endomorphisms of
is an arbitrary subalgebra of the Lie algebra of all endomorphisms of 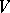 , there is a smallest algebraic Lie algebra containing
, there is a smallest algebraic Lie algebra containing 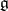 ; it is called the algebraic envelope (or hull) of the Lie subalgebra
; it is called the algebraic envelope (or hull) of the Lie subalgebra 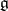 . For a Lie algebra
. For a Lie algebra 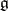 over an arbitrary algebraically closed field
over an arbitrary algebraically closed field 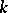 to be algebraic it is necessary that together with every linear operator
to be algebraic it is necessary that together with every linear operator 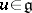 its semi-simple and nilpotent components
its semi-simple and nilpotent components  and
and  should lie in
should lie in 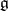 (see Jordan decomposition). This condition determines the so-called almost-algebraic Lie algebras. However, it is not sufficient in order that
(see Jordan decomposition). This condition determines the so-called almost-algebraic Lie algebras. However, it is not sufficient in order that 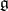 be an algebraic Lie algebra. In the case of a field
be an algebraic Lie algebra. In the case of a field 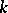 of characteristic 0, a necessary and sufficient condition for a Lie algebra
of characteristic 0, a necessary and sufficient condition for a Lie algebra 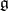 to be algebraic is that, together with
to be algebraic is that, together with  and
and 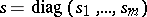 , all operators of the form
, all operators of the form 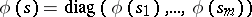 should lie in
should lie in 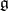 , where
, where 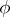 is an arbitrary
is an arbitrary  -linear mapping from
-linear mapping from 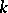 into
into 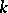 . The structure of an algebraic algebra has been investigated
. The structure of an algebraic algebra has been investigated
in the case of a field of characteristic 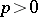 .
.
A Lie algebra 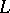 over a commutative ring
over a commutative ring 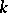 in which for any element
in which for any element 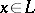 the adjoint transformation
the adjoint transformation  defined on
defined on 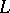 is the root of some polynomial with leading coefficient 1 and remaining coefficients from
is the root of some polynomial with leading coefficient 1 and remaining coefficients from 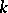 . A finite-dimensional Lie algebra over a field
. A finite-dimensional Lie algebra over a field 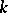 is an algebraic Lie algebra. The converse is false: Over any field
is an algebraic Lie algebra. The converse is false: Over any field 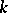 there are infinite-dimensional algebraic Lie algebras with finitely many generators [4]. A number of questions about algebraic Lie algebras have been solved in the class of nil Lie algebras (cf. Lie algebra, nil).
there are infinite-dimensional algebraic Lie algebras with finitely many generators [4]. A number of questions about algebraic Lie algebras have been solved in the class of nil Lie algebras (cf. Lie algebra, nil).
References
| [1] | A. Borel, "Linear algebraic groups" , Benjamin (1969) |
| [2] | C. Chevalley, "Théorie des groupes de Lie" , 2 , Hermann (1951) |
| [3] | G.B. Seligman, "Modular Lie algebras" , Springer (1967) |
| [4] | E.S. Golod, "On nil algebras and residually finite groups" Izv. Akad. Nauk SSSR Ser. Mat. , 28 : 2 (1964) pp. 273–276 (In Russian) |
Comments
References
| [a1] | G.P. Hochschild, "Basic theory of algebraic groups and Lie algebras" , Springer (1981) |
Lie algebra, algebraic. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lie_algebra,_algebraic&oldid=14719