Levi problem
The problem of the geometric characterization of domains in a given analytic space that are Stein spaces (cf. Stein space); it was posed by E.E. Levi [1] for domains in the affine space 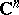 in the following form. Let
in the following form. Let 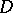 be a domain in
be a domain in 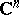 each boundary point
each boundary point 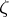 of which has the following property: there is a neighbourhood
of which has the following property: there is a neighbourhood 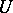 of
of  in
in  and a holomorphic function in
and a holomorphic function in 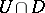 that cannot be extended holomorphically to
that cannot be extended holomorphically to 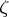 . Is
. Is 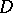 a domain of holomorphy? This property is equivalent to any of the following assertions about the domain
a domain of holomorphy? This property is equivalent to any of the following assertions about the domain 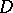 : 1) for no
: 1) for no 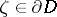 is there a sequence of bounded holomorphic surfaces
is there a sequence of bounded holomorphic surfaces 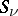 that converges to a holomorphic surface
that converges to a holomorphic surface 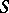 with
with 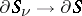 ,
, 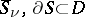 ,
, 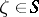 ; 2) the domain
; 2) the domain 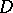 is pseudo-convex, that is,
is pseudo-convex, that is, 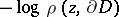 ,
, 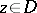 , where
, where 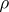 is the Euclidean distance, is a plurisubharmonic function in
is the Euclidean distance, is a plurisubharmonic function in  ; and 3)
; and 3)  is a pseudo-convex manifold, that is, there is in
is a pseudo-convex manifold, that is, there is in 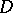 a plurisubharmonic function that tends to
a plurisubharmonic function that tends to 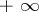 as
as 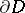 is approached. The Levi problem for
is approached. The Levi problem for 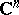 was affirmatively solved in 1953–1954 independently by K. Oka, H. Bremermann and F. Norguet, and Oka solved the problem in a more general formulation, concerned with domains spread over
was affirmatively solved in 1953–1954 independently by K. Oka, H. Bremermann and F. Norguet, and Oka solved the problem in a more general formulation, concerned with domains spread over 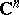 (cf. Covering domain) (see –[6]). Oka's result has been generalized to domains spread over any Stein manifold: If such a domain
(cf. Covering domain) (see –[6]). Oka's result has been generalized to domains spread over any Stein manifold: If such a domain 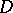 is a pseudo-convex manifold, then
is a pseudo-convex manifold, then 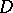 is a Stein manifold. The Levi problem has also been affirmatively solved in a number of other cases, for example, for non-compact domains spread over the projective space
is a Stein manifold. The Levi problem has also been affirmatively solved in a number of other cases, for example, for non-compact domains spread over the projective space  or over a Kähler manifold on which there exists a strictly plurisubharmonic function (see ), and for domains in a Kähler manifold with positive holomorphic bisectional curvature [7]. At the same time, examples of pseudo-convex manifolds and domains are known that are not Stein manifolds and not even holomorphically convex. A necessary and sufficient condition for a complex space to be a Stein space is that it is strongly pseudo-convex (see Pseudo-convex and pseudo-concave). Also, a strongly pseudo-convex domain in any complex space is holomorphically convex and is a proper modification of a Stein space (see , [4] and also Modification; Proper morphism).
or over a Kähler manifold on which there exists a strictly plurisubharmonic function (see ), and for domains in a Kähler manifold with positive holomorphic bisectional curvature [7]. At the same time, examples of pseudo-convex manifolds and domains are known that are not Stein manifolds and not even holomorphically convex. A necessary and sufficient condition for a complex space to be a Stein space is that it is strongly pseudo-convex (see Pseudo-convex and pseudo-concave). Also, a strongly pseudo-convex domain in any complex space is holomorphically convex and is a proper modification of a Stein space (see , [4] and also Modification; Proper morphism).
The Levi problem can also be posed for domains  in an infinite-dimensional complex topological vector space
in an infinite-dimensional complex topological vector space 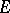 . If
. If 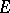 is locally convex and
is locally convex and 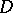 is a domain of holomorphy, then
is a domain of holomorphy, then 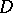 is pseudo-convex, that is, in
is pseudo-convex, that is, in 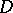 there is a plurisubharmonic function that tends to
there is a plurisubharmonic function that tends to 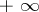 as
as 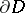 is approached. The converse theorem is false even in Banach spaces, but it has been proved for Banach spaces with a countable basis, as well as for a number of other classes of spaces
is approached. The converse theorem is false even in Banach spaces, but it has been proved for Banach spaces with a countable basis, as well as for a number of other classes of spaces 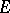 (see ).
(see ).
References
| [1] | E.E. Levi, "Sulle superficie dello spazio a 4 dimensione che possono essere frontiera del campo di esistenza di una funzione analitica di due variabili complesse" Ann. Mat. Pura Appl. , 18 (1911) pp. 69–79 |
| [2a] | A.L. Onishchik, "Stein spaces" J. Soviet Math. , 4 : 5 (1975) pp. 540–554 Itogi Nauk. i Tekhn. Algebra Topol. Geom. , 11 (1974) pp. 125–151 |
| [2b] | A.L. Onishchik, "Pseudoconvexity in the theory of complex spaces" J. Soviet Math. , 14 : 4 (1980) pp. 1363–1407 Itogi Nauk. i Tekhn. Algebra Topol. Geom. , 15 (1977) pp. 93–171 |
| [3] | V.S. Vladimirov, "Methods of the theory of functions of several complex variables" , M.I.T. (1966) (Translated from Russian) |
| [4] | R.C. Gunning, H. Rossi, "Analytic functions of several complex variables" , Prentice-Hall (1965) |
| [5] | B.A. Fuks, "Special chapters in the theory of analytic functions of several complex variables" , Amer. Math. Soc. (1965) (Translated from Russian) |
| [6] | B.V. Shabat, "Introduction of complex analysis" , 2 , Moscow (1976) (In Russian) |
| [7] | O. Suzuki, "Pseudoconvex domains on a Kähler manifold with positive holomorphic, bisectional curvature" Publ. Res. Inst. Math. Sci. Kyoto Univ. , 12 (1976) pp. 191–214; 439–445 |
Comments
References
| [a1] | S. Kobayashi, H. Wu, "Complex differential geometry" , Birkhäuser (1983) |
Levi problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Levi_problem&oldid=14269