Levi-Mal'tsev decomposition
The presentation of a finite-dimensional Lie algebra 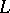 over a field of characteristic zero as a direct sum (as vector spaces) of its radical
over a field of characteristic zero as a direct sum (as vector spaces) of its radical 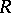 (the maximal solvable ideal in
(the maximal solvable ideal in 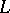 ) and a semi-simple Lie subalgebra
) and a semi-simple Lie subalgebra 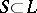 . It was obtained by E.E. Levi [1] and A.I. Mal'tsev [2]. The Levi–Mal'tsev theorem states that there always is such a decomposition
. It was obtained by E.E. Levi [1] and A.I. Mal'tsev [2]. The Levi–Mal'tsev theorem states that there always is such a decomposition 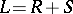 ; moreover, the subalgebra
; moreover, the subalgebra 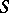 is unique up to an automorphism of the form
is unique up to an automorphism of the form 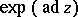 , where
, where 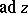 is the inner derivation of the Lie algebra
is the inner derivation of the Lie algebra 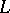 determined by an element
determined by an element  of the nil radical (the largest nilpotent ideal) of
of the nil radical (the largest nilpotent ideal) of 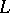 . If
. If 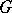 is a connected and simply-connected real Lie group, then there are closed simply-connected analytic subgroups
is a connected and simply-connected real Lie group, then there are closed simply-connected analytic subgroups 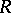 and
and 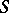 of
of 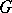 , where
, where 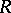 is the maximal connected closed solvable normal subgroup of
is the maximal connected closed solvable normal subgroup of 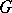 ,
, 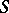 is a semi-simple subgroup of
is a semi-simple subgroup of 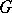 ,
, 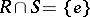 , such that the mapping
, such that the mapping 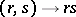 ,
, 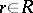 ,
, 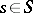 , is an analytic isomorphism of the manifold
, is an analytic isomorphism of the manifold 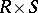 onto
onto 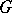 ; in this case the decomposition
; in this case the decomposition 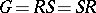 is also called a Levi–Mal'tsev decomposition.
is also called a Levi–Mal'tsev decomposition.
References
| [1] | E.E. Levi, Atti. Accad. Sci. Torino Cl. Sci. Fis. Mat. Natur. , 40 (1906) pp. 3–17 |
| [2] | A.I. Mal'tsev, "On the representation of an algebra as a direct sum of the radical and a semi-simple subalgebra" Dokl. Akad. Nauk SSSR , 36 : 2 (1942) pp. 42–45 (In Russian) |
| [3] | N. Jacobson, "Lie algebras" , Interscience (1962) ((also: Dover, reprint, 1979)) |
| [4] | A.A. Kirillov, "Elements of the theory of representations" , Springer (1976) (Translated from Russian) |
| [5] | M.A. Naimark, "Theory of group representations" , Springer (1982) (Translated from Russian) |
Comments
The existence of 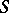 , called the Levi factor (if
, called the Levi factor (if 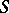 is a semi-simple subalgebra, respectively a semi-simple subgroup, also called a Levi subalgebra, respectively Levi subgroup), was established by Levi. The conjugacy of Levi factors was proved by Mal'tsev.
is a semi-simple subalgebra, respectively a semi-simple subgroup, also called a Levi subalgebra, respectively Levi subgroup), was established by Levi. The conjugacy of Levi factors was proved by Mal'tsev.
An analogue of the decomposition 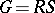 holds for an algebraic group
holds for an algebraic group 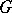 . In this case
. In this case 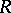 is the maximal unipotent normal subgroup and
is the maximal unipotent normal subgroup and 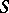 is a maximal reductive subgroup (Mostow's theorem).
is a maximal reductive subgroup (Mostow's theorem).
References
| [a1] | N. Bourbaki, "Elements of mathematics. Lie groups and Lie algebras" , Addison-Wesley (1975) (Translated from French) |
| [a2] | G. Hochschild, "The structure of Lie groups" , Holden-Day (1965) |
Levi-Mal'tsev decomposition. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Levi-Mal%27tsev_decomposition&oldid=13544