Leopoldt conjecture
Let  be a totally real algebraic number field (cf. also Field; Algebraic number) and let
be a totally real algebraic number field (cf. also Field; Algebraic number) and let  be a prime number. Let
be a prime number. Let  denote the distinct embeddings of
denote the distinct embeddings of  into the completion
into the completion  of the algebraic closure of
of the algebraic closure of  . By the Dirichlet unit theorem (cf. also Dirichlet theorem), the unit group
. By the Dirichlet unit theorem (cf. also Dirichlet theorem), the unit group  of
of  has rank
has rank  . Let
. Let  be a
be a 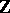 -basis of
-basis of  . In [a5], H.-W. Leopoldt defined the
. In [a5], H.-W. Leopoldt defined the  -adic regulator
-adic regulator 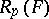 as the
as the 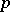 -adic analogue of the Dirichlet regulator:
-adic analogue of the Dirichlet regulator:
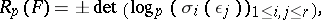 |
where 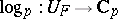 denotes the
denotes the  -adic logarithm.
-adic logarithm.
Leopoldt's conjecture is:  .
.
The definition of 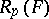 (and therefore also the conjecture) extends to arbitrary number fields (cf. [a7]) and is nowadays considered in this generality. A. Brumer used transcendental methods developed by A. Baker to prove Leopoldt's conjecture for fields
(and therefore also the conjecture) extends to arbitrary number fields (cf. [a7]) and is nowadays considered in this generality. A. Brumer used transcendental methods developed by A. Baker to prove Leopoldt's conjecture for fields 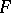 that are Abelian over
that are Abelian over  or over an imaginary quadratic field [a2]. For specific non-Abelian fields the conjecture has also been verified (cf., e.g., [a1]), but in general it is still (1996) open.
or over an imaginary quadratic field [a2]. For specific non-Abelian fields the conjecture has also been verified (cf., e.g., [a1]), but in general it is still (1996) open.
For a totally real field 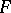 , Leopoldt's conjecture is equivalent to the non-vanishing of the
, Leopoldt's conjecture is equivalent to the non-vanishing of the  -adic
-adic 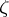 -function
-function 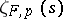 at
at 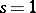 (cf. [a5], [a3]).
(cf. [a5], [a3]).
For a prime  in
in 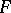 , let
, let 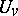 denote the group of units of the local field
denote the group of units of the local field 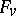 . There is a canonical mapping
. There is a canonical mapping
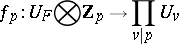 |
and the Leopoldt defect 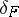 is defined as the
is defined as the  -rank of
-rank of 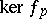 . Class field theory yields the following equivalent formulation of the Leopoldt conjecture (cf. [a7]): Leopoldt's conjecture holds if and only if
. Class field theory yields the following equivalent formulation of the Leopoldt conjecture (cf. [a7]): Leopoldt's conjecture holds if and only if 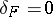 .
.
Relation to Iwasawa theory.
An extension 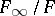 of a number field
of a number field 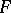 is called a
is called a  -extension if it is a Galois extension and
-extension if it is a Galois extension and  . The number of independent
. The number of independent 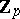 -extensions of
-extensions of 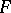 is related via class field theory to the
is related via class field theory to the 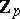 -rank of
-rank of  and is equal to
and is equal to 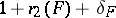 (cf. [a4]), where
(cf. [a4]), where 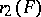 is the number of pairs of complex-conjugate embeddings of
is the number of pairs of complex-conjugate embeddings of 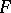 .
.
For 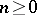 , let
, let 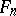 denote the unique subfield of
denote the unique subfield of 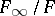 of degree
of degree 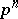 over
over 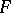 and let
and let 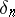 denote the Leopoldt defect of
denote the Leopoldt defect of 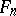 . The
. The  -extension
-extension 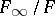 satisfies the weak Leopoldt conjecture if the defects
satisfies the weak Leopoldt conjecture if the defects 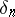 are bounded independent of
are bounded independent of  . It is known (cf. [a4]) that the weak Leopoldt conjecture holds for the so-called cyclotomic
. It is known (cf. [a4]) that the weak Leopoldt conjecture holds for the so-called cyclotomic  -extension of
-extension of  , i.e. for the unique
, i.e. for the unique  -extension contained in
-extension contained in 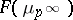 .
.
Relation to Galois cohomology.
Let 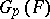 denote the Galois group of the maximal pro-
denote the Galois group of the maximal pro-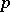 -extension of
-extension of  , which is unramified outside
, which is unramified outside 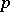 . Leopoldt's conjecture is equivalent to the vanishing of the Galois cohomology group
. Leopoldt's conjecture is equivalent to the vanishing of the Galois cohomology group  [a6]. More generally, it is conjectured that
[a6]. More generally, it is conjectured that
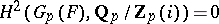 |
for all  [a6]. This is known to be true for
[a6]. This is known to be true for 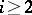 as a consequence of a profound result of A. Borel in algebraic
as a consequence of a profound result of A. Borel in algebraic 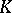 -theory.
-theory.
References
| [a1] | F. Bertrandias, J.-J. Payan, "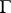 -extensions et invariants cyclotomiques" Ann. Sci. Ecole Norm. Sup. (4) , 5 (1972) pp. 517–543 -extensions et invariants cyclotomiques" Ann. Sci. Ecole Norm. Sup. (4) , 5 (1972) pp. 517–543 |
| [a2] | A. Brumer, "On the units of algebraic number fields" Mathematica , 14 (1967) pp. 121–124 |
| [a3] | P. Colmez, "Résidu en 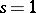 des fonctions zêta des fonctions zêta 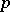 -adiques" Invent. Math. , 91 (1988) pp. 371–389 -adiques" Invent. Math. , 91 (1988) pp. 371–389 |
| [a4] | K. Iwasawa, "On 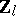 -extensions of algebraic number fields" Ann. of Math. , 98 (1973) pp. 246–326 -extensions of algebraic number fields" Ann. of Math. , 98 (1973) pp. 246–326 |
| [a5] | H.-W. Leopoldt, "Zur Arithmetik in abelschen Zahlkörpern" J. Reine Angew. Math. , 209 (1962) pp. 54–71 |
| [a6] | P. Schneider, "Über gewisse Galoiscohomologiegruppen" Math. Z. , 168 (1979) pp. 181–205 |
| [a7] | L.C. Washington, "Introduction to cyclotomic fields" , Springer (1982) |
Leopoldt conjecture. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Leopoldt_conjecture&oldid=16297