Legendre symbol
An arithmetic function of the numbers 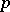 and
and  , defined for odd prime numbers
, defined for odd prime numbers 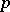 and integers
and integers  not divisible by
not divisible by 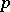 . The Legendre symbol is denoted by
. The Legendre symbol is denoted by  . The Legendre symbol
. The Legendre symbol 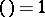 if the congruence
if the congruence 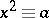
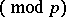 is solvable; otherwise,
is solvable; otherwise, 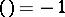 . The Legendre symbol is sometimes defined for numbers
. The Legendre symbol is sometimes defined for numbers  divisible by
divisible by  by putting
by putting 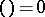 in this case. The Legendre symbol has the following properties:
in this case. The Legendre symbol has the following properties:
1) if 
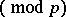 , then
, then 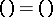 ;
;
2) 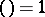 ;
;
3) 
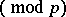 ;
;
4)  ;
;
5) 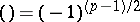 ;
;
6) 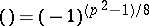 ;
;
7) if  and
and 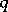 are odd prime numbers, then
are odd prime numbers, then
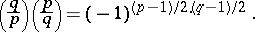 |
The last fact, first proved by C.F. Gauss (1796), is called the quadratic reciprocity law. The above properties make it possible to calculate the Legendre symbol easily, without resorting to solving congruences. For example,
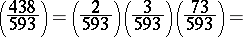 |
 |
The calculation of the Legendre symbol is facilitated still more by the use of the Jacobi symbol. For fixed 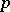 the Legendre symbol is a real character of the multiplicative group of residue classes modulo
the Legendre symbol is a real character of the multiplicative group of residue classes modulo 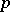 (cf. Character of a group).
(cf. Character of a group).
It was introduced by A.M. Legendre in 1785.
References
| [1] | I.M. Vinogradov, "Elements of number theory" , Dover, reprint (1954) (Translated from Russian) |
Comments
References
| [a1] | G.H. Hardy, E.M. Wright, "An introduction to the theory of numbers" , Oxford Univ. Press (1979) |
Legendre symbol. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Legendre_symbol&oldid=14735