Legendre functions
From Encyclopedia of Mathematics
Functions that are solutions of the Legendre equation
 | (*) |
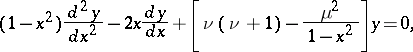where 
and 
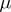are arbitrary numbers. If 
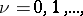and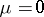 
, then the solutions of equation (*), restricted to 
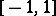, are called Legendre polynomials; for integers 
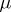with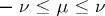 
, the solutions of equation (*), restricted to 
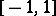, are called Legendre associated functions.
Comments
References
| [a1] | M. Abramowitz, I.A. Stegun, "Handbook of mathematical functions" , Dover, reprint (1965) pp. Chapt. 8 |
| [a2] | N.N. Lebedev, "Special functions and their applications" , Dover, reprint (1972) (Translated from Russian) |
How to Cite This Entry:
Legendre functions. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Legendre_functions&oldid=15230
Legendre functions. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Legendre_functions&oldid=15230
This article was adapted from an original article by A.B. Ivanov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article