Lefschetz duality
From Encyclopedia of Mathematics
Lefschetz–Poincaré duality
An assertion about the duality between homology and cohomology, established by S. Lefschetz. More precisely, if 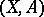 is a pair of spaces such that
is a pair of spaces such that 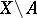 is an
is an  -dimensional topological manifold, then for any Abelian group
-dimensional topological manifold, then for any Abelian group 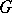 and any
and any 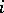 there is an isomorphism
there is an isomorphism
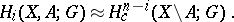 |
On the right-hand side one has cohomology with compact support. If the manifold 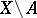 is non-orientable, one must, as usual, take cohomology with local coefficients.
is non-orientable, one must, as usual, take cohomology with local coefficients.
Comments
The original reference is [a1]. Good modern accounts of Lefschetz duality can be found in [a2] and (from the point of view of sheaf cohomology) in [a3].
References
| [a1] | S. Lefschetz, "Manifolds with a boundary and their transformations" Trans. Amer. Math. Soc. , 29 (1927) pp. 429–462 |
| [a2] | C.R.F. Maunder, "Algebraic topology" , Cambridge Univ. Press, reprint (1980) |
| [a3] | B. Iversen, "Cohomology of sheaves" , Springer (1986) |
How to Cite This Entry:
Lefschetz duality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lefschetz_duality&oldid=11981
Lefschetz duality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lefschetz_duality&oldid=11981
This article was adapted from an original article by Yu.B. Rudyak (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article