Lebesgue space
A measure space  (where
(where  is a set,
is a set, 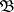 is a
is a  -algebra of subsets of
-algebra of subsets of  , called measurable sets, and
, called measurable sets, and  is a measure defined on the measurable sets), isomorphic to the "standard model" , consisting of an interval
is a measure defined on the measurable sets), isomorphic to the "standard model" , consisting of an interval  and an at most countable set of points
and an at most countable set of points  (in "extreme" cases this "model" may consists of just the interval
(in "extreme" cases this "model" may consists of just the interval  or of just the points
or of just the points  ) endowed with the following measure
) endowed with the following measure  : on
: on  one takes the usual Lebesgue measure, and to each of the points
one takes the usual Lebesgue measure, and to each of the points 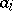 one ascribes a measure
one ascribes a measure 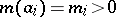 ; the measure is assumed to be normalized, that is,
; the measure is assumed to be normalized, that is,  . The "isomorphism" can be understood here in the strict sense or modulo
. The "isomorphism" can be understood here in the strict sense or modulo  ; one obtains, respectively, a narrower or wider version of the concept of a Lebesgue space (in the latter case one can talk about a Lebesgue space modulo
; one obtains, respectively, a narrower or wider version of the concept of a Lebesgue space (in the latter case one can talk about a Lebesgue space modulo  ). One can give a definition of a Lebesgue space in terms of "intrinsic" properties of the measure space
). One can give a definition of a Lebesgue space in terms of "intrinsic" properties of the measure space  (see [1]–[3]).
(see [1]–[3]).
A Lebesgue space is the most frequently occurring type of space with a normalized measure, since any complete separable metric space with a normalized measure (defined on its Borel subsets and then completed in the usual way) is a Lebesgue space. Apart from properties common to all measure spaces, a Lebesgue space has a number of specific "good" properties. For example, any automorphism of a Boolean  -algebra on a measure space
-algebra on a measure space 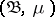 is generated by some automorphism of a Lebesgue space
is generated by some automorphism of a Lebesgue space 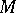 . Under a number of natural operations, from a Lebesgue space one again obtains a Lebesgue space. Thus, a subset
. Under a number of natural operations, from a Lebesgue space one again obtains a Lebesgue space. Thus, a subset  of positive measure in a Lebesgue space
of positive measure in a Lebesgue space  is itself a Lebesgue space (its measurable subsets are assumed to be those that are measurable in
is itself a Lebesgue space (its measurable subsets are assumed to be those that are measurable in 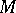 , and the measure is
, and the measure is  ); the direct product of finitely or countably many Lebesgue spaces is a Lebesgue space. Other properties of Lebesgue spaces are connected with measurable partitions (cf. Measurable decomposition).
); the direct product of finitely or countably many Lebesgue spaces is a Lebesgue space. Other properties of Lebesgue spaces are connected with measurable partitions (cf. Measurable decomposition).
References
| [1] | P.R. Halmos, J. von Neumann, "Operator methods in classical mechanics. II" Ann. of Math. , 43 : 2 (1942) pp. 332–350 |
| [2] | V.A. Rokhlin, "On mean notions of measure theory" Mat. Sb. , 25 : 1 (1949) pp. 107–150 (In Russian) |
| [3] | J. Haezendonck, "Abstract Lebesgue–Rokhlin spaces" Bull. Soc. Math. Belg. , 25 : 3 (1973) pp. 243–258 |
Comments
Cf. also [a1] for a discussion of Lebesgue spaces and measurable partitions, including an intrinsic description of Lebesgue spaces.
References
| [a1] | I.P. [I.P. Kornfel'd] Cornfel'd, S.V. Fomin, Ya.G. Sinai, "Ergodic theory" , Springer (1982) pp. Appendix 1 (Translated from Russian) |
Lebesgue space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lebesgue_space&oldid=11259