Lebesgue integral
The most important generalization of the concept of an integral. Let  be a space with a non-negative complete countably-additive measure
be a space with a non-negative complete countably-additive measure  (cf. Countably-additive set function; Measure space), where
(cf. Countably-additive set function; Measure space), where  . A simple function is a measurable function
. A simple function is a measurable function  that takes at most a countable set of values:
that takes at most a countable set of values:  ,
,  for
for  , if
, if  ,
,  . A simple function
. A simple function 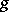 is said to be summable if the series
is said to be summable if the series
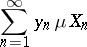 |
converges absolutely (cf. Absolutely convergent series); the sum of this series is the Lebesgue integral
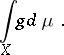 |
A function 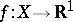 is summable on
is summable on 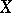 ,
, 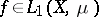 , if there is a sequence of simple summable functions
, if there is a sequence of simple summable functions 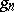 uniformly convergent (cf. Uniform convergence) to
uniformly convergent (cf. Uniform convergence) to 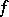 on a set of full measure, and if the limit
on a set of full measure, and if the limit
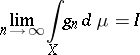 |
is finite. The number 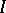 is the Lebesgue integral
is the Lebesgue integral
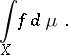 |
This is well-defined: the limit 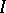 exists and does not depend on the choice of the sequence
exists and does not depend on the choice of the sequence 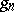 . If
. If 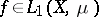 , then
, then 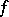 is a measurable almost-everywhere finite function on
is a measurable almost-everywhere finite function on 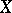 . The Lebesgue integral is a linear non-negative functional on
. The Lebesgue integral is a linear non-negative functional on 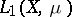 with the following properties:
with the following properties:
1) if 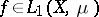 and if
and if
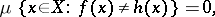 |
then 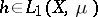 and
and
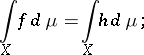 |
2) if  , then
, then 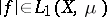 and
and
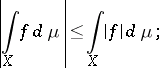 |
3) if 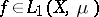 ,
, 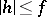 and
and 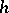 is measurable, then
is measurable, then 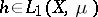 and
and
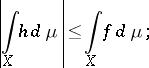 |
4) if 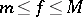 and
and  is measurable, then
is measurable, then 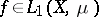 and
and
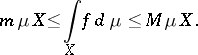 |
In the case when 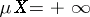 and
and 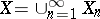 ,
, 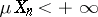 , the Lebesgue integral is defined as
, the Lebesgue integral is defined as
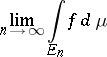 |
under the condition that this limit exists and is finite for any sequence 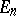 such that
such that 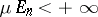 ,
, 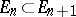 ,
,  . In this case the properties 1), 2), 3) are preserved, but condition 4) is violated.
. In this case the properties 1), 2), 3) are preserved, but condition 4) is violated.
For the transition to the limit under the Lebesgue integral sign see Lebesgue theorem.
If 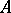 is a measurable set in
is a measurable set in 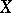 , then the Lebesgue integral
, then the Lebesgue integral
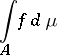 |
is defined either as above, by replacing 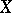 by
by 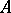 , or as
, or as
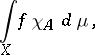 |
where 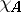 is the characteristic function of
is the characteristic function of 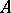 ; these definitions are equivalent. If
; these definitions are equivalent. If 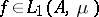 , then
, then 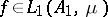 for any measurable
for any measurable 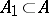 . If
. If
 |
if 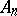 is measurable for every
is measurable for every  , if
, if
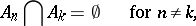 |
and if 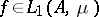 , then
, then
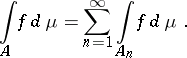 |
Conversely, if under these conditions on 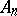 one has
one has 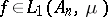 for every
for every  and if
and if
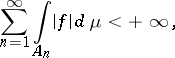 |
then  and the previous equality is true (
and the previous equality is true ( -additivity of the Lebesgue integral).
-additivity of the Lebesgue integral).
The function of sets  given by
given by
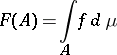 |
is absolutely continuous with respect to 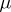 (cf. Absolute continuity); if
(cf. Absolute continuity); if  , then
, then 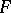 is a non-negative measure that is absolutely continuous with respect to
is a non-negative measure that is absolutely continuous with respect to 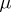 . The converse assertion is the Radon–Nikodým theorem.
. The converse assertion is the Radon–Nikodým theorem.
For functions 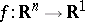 the name "Lebesgue integral" is applied to the corresponding functional if the measure
the name "Lebesgue integral" is applied to the corresponding functional if the measure 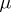 is the Lebesgue measure; here, the set of summable functions is denoted simply by
is the Lebesgue measure; here, the set of summable functions is denoted simply by 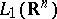 , and the integral by
, and the integral by
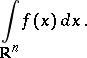 |
For other measures this functional is called a Lebesgue–Stieltjes integral.
If 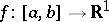 ,
, 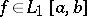 and if
and if 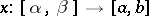 is a non-decreasing absolutely continuous function, then
is a non-decreasing absolutely continuous function, then
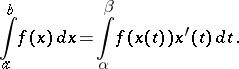 |
If 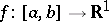 ,
, 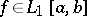 and if
and if 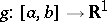 is monotone on
is monotone on 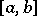 , then
, then 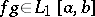 and there is a point
and there is a point 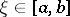 such that
such that
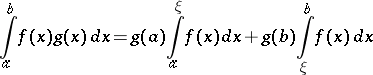 |
(the second mean-value theorem).
In 1902 H. Lebesgue gave (see [1]) a definition of the integral for 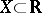 and measure
and measure 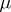 equal to the Lebesgue measure. He constructed simple functions that uniformly approximate almost-everywhere on a set
equal to the Lebesgue measure. He constructed simple functions that uniformly approximate almost-everywhere on a set 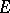 of finite measure a measurable non-negative function
of finite measure a measurable non-negative function 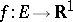 , and proved the existence of a common limit (finite or infinite) of the integrals of these simple functions as they tend to
, and proved the existence of a common limit (finite or infinite) of the integrals of these simple functions as they tend to 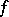 . The Lebesgue integral is a basis for various generalizations of the concept of an integral. As N.N. Luzin remarked [2], property 2), called absolute integrability, distinguishes the Lebesgue integral for
. The Lebesgue integral is a basis for various generalizations of the concept of an integral. As N.N. Luzin remarked [2], property 2), called absolute integrability, distinguishes the Lebesgue integral for 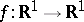 from all possible generalized integrals.
from all possible generalized integrals.
References
| [1] | H. Lebesgue, "Leçons sur l'intégration et la récherche des fonctions primitives" , Gauthier-Villars (1928) |
| [2] | N.N. Luzin, "The integral and trigonometric series" , Moscow-Leningrad (1915) (In Russian) (Thesis; also: Collected Works, Vol. 1, Moscow, 1953, pp. 48–212) |
| [3] | A.N. Kolmogorov, S.V. Fomin, "Elements of the theory of functions and functional analysis" , 1–2 , Graylock (1957–1961) (Translated from Russian) |
Comments
For other generalizations of the notion of an integral see  -integral; Bochner integral; Boks integral; Burkill integral; Daniell integral; Darboux sum; Denjoy integral; Kolmogorov integral; Perron integral; Perron–Stieltjes integral; Pettis integral; Radon integral; Stieltjes integral; Strong integral; Wiener integral. See also, of course, Riemann integral. See also Double integral; Improper integral; Fubini theorem (on changing the order of integration).
-integral; Bochner integral; Boks integral; Burkill integral; Daniell integral; Darboux sum; Denjoy integral; Kolmogorov integral; Perron integral; Perron–Stieltjes integral; Pettis integral; Radon integral; Stieltjes integral; Strong integral; Wiener integral. See also, of course, Riemann integral. See also Double integral; Improper integral; Fubini theorem (on changing the order of integration).
References
| [a1] | P.R. Halmos, "Measure theory" , v. Nostrand (1950) |
| [a2] | I.N. Pesin, "Classical and modern integration theories" , Acad. Press (1970) (Translated from Russian) |
| [a3] | S. Saks, "Theory of the integral" , Hafner (1952) (Translated from French) |
| [a4] | H.L. Royden, "Real analysis" , Macmillan (1968) |
| [a5] | W. Rudin, "Real and complex analysis" , McGraw-Hill (1978) pp. 24 |
| [a6] | E. Hewitt, K.R. Stromberg, "Real and abstract analysis" , Springer (1965) |
Lebesgue integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lebesgue_integral&oldid=18585