Lebedev transform
From Encyclopedia of Mathematics
The integral transform
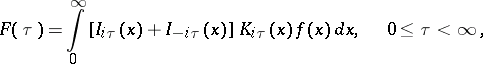 |
where 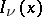 and
and  are the modified cylinder functions. It was introduced by N.N. Lebedev [1]. If
are the modified cylinder functions. It was introduced by N.N. Lebedev [1]. If
 |
then for almost-all  one has the inversion formula
one has the inversion formula
 |
References
| [1] | N.N. Lebedev, "On an integral representation of an arbitrary function in terms of squares of MacDonald functions with imaginary index" Sibirsk. Mat. Zh. , 3 : 2 (1962) pp. 213–222 (In Russian) |
Comments
The following transform pair is also called a Lebedev transform (or Kontorovich–Lebedev transform)
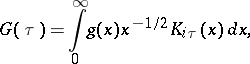 |
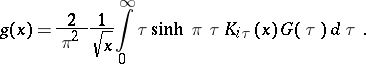 |
References
| [a1] | N.N. Lebedev, "Special functions and their applications" , Prentice-Hall (1965) (Translated from Russian) |
| [a2] | I.N. Sneddon, "The use of integral transforms" , McGraw-Hill (1972) pp. Chapt. 6 |
How to Cite This Entry:
Lebedev transform. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lebedev_transform&oldid=16220
Lebedev transform. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lebedev_transform&oldid=16220
This article was adapted from an original article by Yu.A. BrychkovA.P. Prudnikov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article