Law of the iterated logarithm
2020 Mathematics Subject Classification: Primary: 60F10 Secondary: 60F15 [MSN][ZBL]
A limit theorem in probability theory which is a refinement of the strong law of large numbers. Let 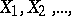 be a sequence of random variables and let
be a sequence of random variables and let
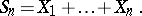 |
For simplicity one assumes that 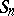 has zero median for each
has zero median for each  . While the theorem on the strong law of large numbers deals with conditions under which
. While the theorem on the strong law of large numbers deals with conditions under which 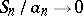 almost surely (
almost surely ( ) for
) for 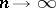 , where
, where 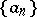 is a sequence of numbers, the theorem on the law of the iterated logarithm deals with sequences of numbers
is a sequence of numbers, the theorem on the law of the iterated logarithm deals with sequences of numbers 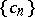 such that
such that
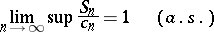 | (1) |
or
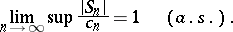 | (2) |
Relation (1) is equivalent to
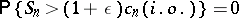 |
and
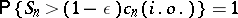 |
for any 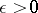 , where
, where 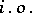 denotes infinitely often.
denotes infinitely often.
Relations of the form of (1) and (2) hold under more restrictive conditions than the estimates implied by the strong law of large numbers. If 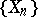 is a sequence of independent random variables having identical distributions with mathematical expectations equal to zero, then
is a sequence of independent random variables having identical distributions with mathematical expectations equal to zero, then
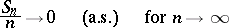 |
(Kolmogorov's theorem); if the additional condition 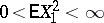 is satisfied, then one has the stronger relation (2), in which
is satisfied, then one has the stronger relation (2), in which
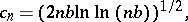 |
where 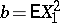 (the Hartman–Wintner theorem).
(the Hartman–Wintner theorem).
The first theorem of general type on the law of the iterated logarithm was the following result obtained by A.N. Kolmogorov [Ko]. Let 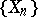 be a sequence of independent random variables with mathematical expectations equal to zero and with finite variances, and let
be a sequence of independent random variables with mathematical expectations equal to zero and with finite variances, and let
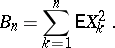 |
If 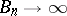 for
for 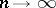 and if there exists a sequence of positive constants
and if there exists a sequence of positive constants 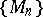 such that
such that
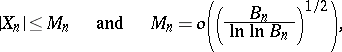 |
then (1) and (2) are satisfied for
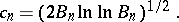 |
In the particular case where 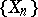 is a sequence of independent random variables having identical distributions with two possible values, this assertion was derived by A.Ya. Khinchin [Kh]. J. Marcinkiewicz and A. Zygmund [MZ] showed that under the conditions of Kolmogorov's theorem one cannot replace
is a sequence of independent random variables having identical distributions with two possible values, this assertion was derived by A.Ya. Khinchin [Kh]. J. Marcinkiewicz and A. Zygmund [MZ] showed that under the conditions of Kolmogorov's theorem one cannot replace  by
by 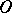 . W. Feller [F] examined a generalization of Kolmogorov's law of the iterated logarithm for sequences of independent bounded non-identically distributed random variables. See [S] for other generalizations of the law; there is also the following result (see [S2]), which is related to the Hartman–Wintner theorem: If
. W. Feller [F] examined a generalization of Kolmogorov's law of the iterated logarithm for sequences of independent bounded non-identically distributed random variables. See [S] for other generalizations of the law; there is also the following result (see [S2]), which is related to the Hartman–Wintner theorem: If 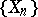 is a sequence of independent random variables having identical distributions with infinite variances, then
is a sequence of independent random variables having identical distributions with infinite variances, then
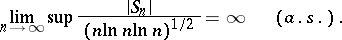 |
The results obtained on the law of the iterated logarithm for sequences of independent random variables have served as a starting point for numerous researches on the applicability of this law to sequences of dependent random variables and vectors and to random processes.
References
| [Ko] | A.N. Kolmogoroff, "Ueber das Gesetz des iterierten Logarithmus" Math. Ann. , 101 (1929) pp. 126–135 |
| [Kh] | A. Khintchine, "Ueber einen Satz der Wahrscheinlichkeitsrechnung" Fund. Math. , 6 (1924) pp. 9–20 Zbl 50.0344.02 |
| [MZ] | J. Marcinkiewicz, A. Zygmund, "Rémarque sur la loi du logarithme itéré" Fund. Math. , 29 (1937) pp. 215–222 Zbl 0018.03204 Zbl 63.1076.03 |
| [F] | W. Feller, "The general form of the so-called law of the iterated logarithm" Trans. Amer. Math. Soc. , 54 (1943) pp. 373–402 MR0009263 Zbl 0063.08417 |
| [S] | V. Strassen, "An invariance principle for the law of the iterated logarithm" Z. Wahrsch. Verw. Geb. , 3 (1964) pp. 211–226 MR0175194 Zbl 0132.12903 |
| [S2] | V. Strassen, "A converse to the law of iterated logarithm" Z. Wahrsch. Verw. Geb. , 4 (1965–1966) pp. 265–268 Zbl 0141.16501 |
| [HW] | P. Hartman, A. Wintner, "On the law of the iterated logarithm" Amer. J. Math. , 63 (1941) pp. 169–176 MR0003497 Zbl 0024.15802 Zbl 67.0460.03 |
| [La] | J. Lamperty, "Probability" , Benjamin (1966) |
| [P] | V.V. Petrov, "Sums of independent random variables" , Springer (1975) (Translated from Russian) MR0388499 Zbl 0322.60043 Zbl 0322.60042 |
Comments
References
| [HH] | P. Hall, C.C. Heyde, "Martingale limit theory and its application" , Acad. Press (1980) MR0624435 Zbl 0462.60045 |
| [F2] | W. Feller, "An introduction to probability theory and its applications" , 1 , Wiley (1968) MR0228020 Zbl 0155.23101 |
| [Lo] | M. Loève, "Probability theory" , Princeton Univ. Press (1963) pp. Chapt. XIV MR0203748 Zbl 0108.14202 |
Law of the iterated logarithm. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Law_of_the_iterated_logarithm&oldid=26553