Lavrent'ev theorem
Lavrent'ev's theorem in descriptive set theory: A topological mapping between two sets in  can be extended to a homeomorphism between certain sets of type
can be extended to a homeomorphism between certain sets of type  containing them. A consequence of this theorem is that the Hausdorff type of a set is a topological invariant (see ).
containing them. A consequence of this theorem is that the Hausdorff type of a set is a topological invariant (see ).
Lavrent'ev's theorem in approximation theory gives a criterion for the possibility of uniform approximation: In order that a function, continuous on a compact set  , can be uniformly approximated on
, can be uniformly approximated on  by polynomials it is necessary and sufficient that
by polynomials it is necessary and sufficient that  is a compact set without interior points that does not partition the complex plane (see ).
is a compact set without interior points that does not partition the complex plane (see ).
Lavrent'ev's theorem in the theory of quasi-conformal mapping: Let  and
and  be two simply-connected domains in the plane bounded by piecewise-smooth curves and let
be two simply-connected domains in the plane bounded by piecewise-smooth curves and let  and
and  be triples of positively enumerated points on their boundaries. Then for any strongly-elliptic system of equations
be triples of positively enumerated points on their boundaries. Then for any strongly-elliptic system of equations
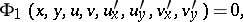 |
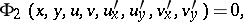 |
with uniformly continuous partial derivatives of the functions that specify the equations of the characteristics, there is always a unique homeomorphic mapping of  onto
onto 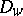 that realizes a solution
that realizes a solution 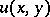 ,
, 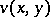 of the system, and under which the given triples of boundary points correspond to each other.
of the system, and under which the given triples of boundary points correspond to each other.
For Lavrent'ev's theorem in mechanics (aerofoil theory, solitary wave, forms of dynamical loss of stability, flows, the theory of cumulative charge, directed detonation) see [4].
Theorems 1)–4) are due to M.A. Lavrent'ev.
References
| [1] | M. [M.A. Lavrent'ev] Lavrentieff, "Contribution à la théorie des ensembles homéomorphes" Fund. Math. , 6 (1924) pp. 149–160 |
| [2] | M.A. Lavrent'ev, Izv. Akad. Nauk SSSR Ser. Mat. , 12 : 6 (1948) pp. 513–554 |
| [3] | M.A. Lavrent'ev, "On the theory of conformal mapping" Tr. Fiz.-Mat. Inst. Akad. Nauk SSSR, Otdel. Mat. , 5 (1934) pp. 195–245 (In Russian) |
| [4] | "Mikhail Alekseevich Lavrent'ev" , Bibliography of Soviet Scientists, Mathematics Series , 12 , Acad. Sci. USSR , Moscow (1971) (In Russian) |
Comments
1) This theorem is valid in the following more general situation: If 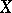 and
and 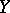 are completely-metrizable spaces,
are completely-metrizable spaces, 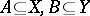 , and
, and 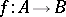 is a homeomorphism, then there are
is a homeomorphism, then there are  sets (cf. Set of type
sets (cf. Set of type 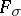 (
( ))
)) 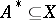 and
and 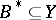 with
with 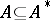 ,
, 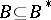 and a homeomorphism
and a homeomorphism 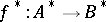 extending
extending 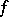 .
.
This theorem has proved to be very useful in extension theory and in the construction of counterexamples.
2) This theorem is subsumed by the Mergelyan theorem. See [a6]–[a8], [a11].
5) Another problem related with the name of Lavrent'ev is as follows.
Consider the following two optimization problems:
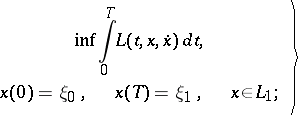 | (a1) |
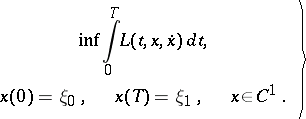 | (a2) |
I.e.  is supposed to be absolutely continuous in (a1) and continuously differentiable in (a2), Then it may happen that
is supposed to be absolutely continuous in (a1) and continuously differentiable in (a2), Then it may happen that 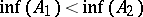 . This is known as the Lavrent'ev phenomenon. As a consequence, the minimizer for (a1) will not satisfy the Euler–Lagrange equation even though
. This is known as the Lavrent'ev phenomenon. As a consequence, the minimizer for (a1) will not satisfy the Euler–Lagrange equation even though 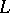 is smooth.
is smooth.
References
| [a1] | J. Aarts, "Completeness degree, a generalization of dimension" Fund. Math. , 63 (1968) pp. 28–41 |
| [a2] | T.A. Chapman, "Dense  -compact subsets of infinite-dimensional manifolds" Trans. Amer. Math. Soc. , 154 (1971) pp. 399–426 -compact subsets of infinite-dimensional manifolds" Trans. Amer. Math. Soc. , 154 (1971) pp. 399–426 |
| [a3] | E.K. van Douwen, "A compact space with a measure that knows which sets are homeomorphic" Adv. Math. , 52 (1984) pp. 1–33 |
| [a4] | R. Engelking, "General topology" , Heldermann (1989) |
| [a5] | J. van Mill, "Domain invariance in infinite-dimensional linear spaces" Proc. Amer. Math. Soc. , 101 (1987) pp. 173–180 |
| [a6] | S.N. Mergelyan, "On a theorem of M.A. Lavrent'ev" Transl. Amer. Math. Soc. , 3 (1962) pp. 281–286 Dokl. Akad. Nauk SSSR , 77 (1951) pp. 565–568 |
| [a7] | S.N. Mergelyan, "On the representation of functions by series of polynomials on closed sets" Transl. Amer. Math. Soc. , 3 (1962) pp. 287–293 Dokl. Akad. Nauk SSSR , 78 (1951) pp. 405–408 |
| [a8] | E.F. Collingwood, A.J. Lohwater, "The theory of cluster sets" , Cambridge Univ. Press (1966) |
| [a9] | L. Cesari, "Optimization - Theory and applications" , Springer (1983) pp. Sect. 18.5 |
| [a10] | M. [M.A. Lavrent'ev] Lavrentiev, "Sur quelques problèmes du calcul des variations" Ann. Mat. Pura Appl. , 4 (1926) pp. 7–28 |
| [a11] | P.J. Davis, "Interpolation and approximation" , Dover, reprint (1975) pp. 278ff |
| [a12] | M.A. Lavrent'ev, "Variational methods for boundary value problems for systems of elliptic equations" , Noordhoff (1963) (Translated from Russian) |
Lavrent'ev theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lavrent%27ev_theorem&oldid=14704