Lattice with complements

complemented lattice

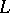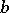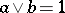A lattice with a zero 0 and a unit 1 in which for any element there is an element (called a complement of the element ) such that and 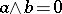. If for any 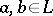with 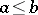the interval 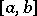is a complemented lattice, then 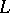is called a relatively complemented lattice. Each complemented modular lattice is a relatively complemented lattice. 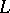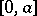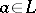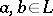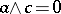A lattice with a zero 0 is called: a) a partially complemented lattice if each of its intervals of the form , , is a complemented lattice; b) a weakly complemented lattice if for any with there is an element such that and 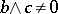; c) a semi-complemented lattice if for any 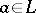, , 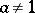there is an element 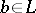, , 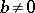such that 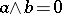; d) a pseudo-complemented lattice if for any 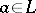there is an element 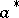such that 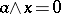if and only if 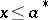; and e) a quasi-complemented lattice if for any 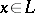there is an element 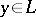such that 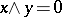and 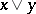is a dense element. Ortho-complemented lattices also play an important role (see Orthomodular lattice). See [4] for the relation between the various types of complements in lattices.

References

[1]	G. Birkhoff, "Lattice theory" , Colloq. Publ. , 25 , Amer. Math. Soc. (1973)
[2]	L.A. Skornyakov, "Elements of lattice theory" , A. Hilger (1977) (Translated from Russian)
[3]	L.A. Skornyakov, "Complemented modular lattices and regular rings" , Oliver & Boyd (1964) (Translated from Russian)
[4]	P.A. Grillet, J.C. Varlet, "Complementedness conditions in lattices" Bull Soc. Roy. Sci. Liège , 36 : 11–12 (1967) pp. 628–642

Comments

In a distributive lattice, each element has at most one complement; conversely, a lattice in which each element has at most one relative complement in each interval in which it lies must be distributive.

References

[a1]	L. Beran, "Orthomodular lattices" , Reidel (1985)
[a2]	G. Grätzer, "Lattice theory" , Freeman (1971)
[a3]	M.L. Dubreil-Jacotin, L. Lesieur, R. Croiset, "Leçons sur la théorie des treilles" , Gauthier-Villars (1953)