Lattice of points

point lattice, in 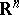, with basis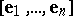

The set of points , where 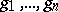are integers.

The lattice 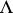can be regarded as the free Abelian group with generators. A lattice has an infinite number of bases; their general form is 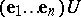, where 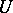runs through all integral matrices of determinant 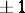. The quantity

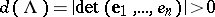is the volume of the parallelopipedon formed by the vectors . It does not depend on the choice of a basis and is called the determinant of the lattice .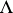

The partition of point lattices into Voronoi lattice types plays an important role in the geometry of quadratic forms (cf. Quadratic form).

Comments

The idea of lattices and lattice points links geometry to arithmetic (integers). Therefore it plays a central role in the geometry of numbers; integer programming (lattice point theorems); Diophantine approximations; reduction theory; analytic number theory; numerical analysis; crystallography (cf. Crystallography, mathematical); coding and decoding; combinatorics; geometric algorithms, and other areas.

References

[a1]	J.W.S. Cassels, "An introduction to the geometry of numbers" , Springer (1972)
[a2]	P. Erdös, P.M. Gruber, J. Hammer, "Lattice points" , Longman (1989)
[a3]	P.M. Gruber, C.G. Lekkerkerker, "Geometry of numbers" , North-Holland (1987) pp. Sect. (iv) (Updated reprint)
[a4]	P.M. Gruber (ed.) J.M. Wills (ed.) , Handbook of convex geometry , North-Holland (1992)
[a5]	R. Kannan, L. Lovasz, "Covering minima and lattice-point-free convex bodies" Ann. of Math. , 128 (1988) pp. 577–602