Lattice-ordered group
 -group
-group
A group  on the set of elements of which a partial-order relation
on the set of elements of which a partial-order relation  is defined possessing the properties: 1)
is defined possessing the properties: 1)  is a lattice relative to
is a lattice relative to  , i.e. for any
, i.e. for any  there are elements
there are elements  ,
,  such that
such that  and
and 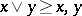 ; for any
; for any 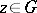 ,
, 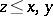 implies
implies 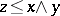 , and for any
, and for any 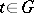 and
and 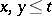 one has
one has 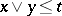 ; and 2) for any
; and 2) for any 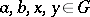 the inequality
the inequality 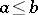 implies
implies 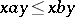 . Similarly, a lattice-ordered group can be defined as an algebraic system of signature
. Similarly, a lattice-ordered group can be defined as an algebraic system of signature  that satisfies the axioms: 3)
that satisfies the axioms: 3)  is a group; 4)
is a group; 4) 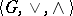 is a lattice; and 5)
is a lattice; and 5) 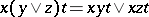 and
and 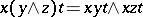 for any
for any 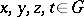 .
.
The lattice of elements of a lattice-ordered group is distributive (cf. Distributive lattice). The absolute value (respectively, the positive and the negative part) of an element  is the element
is the element 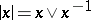 (respectively,
(respectively,  and
and 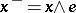 ). In lattice-ordered groups, the following relations hold:
). In lattice-ordered groups, the following relations hold:
 |
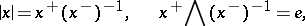 |
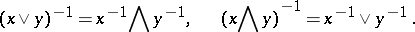 |
Two elements  and
and 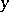 are called orthogonal if
are called orthogonal if 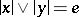 . Orthogonal elements commute.
. Orthogonal elements commute.
A subset 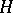 of an
of an 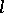 -group
-group 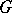 is called an
is called an 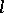 -subgroup if
-subgroup if  is a subgroup and a sublattice in
is a subgroup and a sublattice in  ; an
; an  -subgroup
-subgroup  is called an
is called an 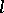 -ideal of
-ideal of 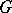 if it is normal and convex in
if it is normal and convex in 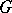 . The set of
. The set of 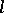 -subgroups of a lattice-ordered group forms a sublattice of the lattice of all its subgroups. The lattice of
-subgroups of a lattice-ordered group forms a sublattice of the lattice of all its subgroups. The lattice of 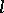 -ideals of a lattice-ordered group is distributive. An
-ideals of a lattice-ordered group is distributive. An 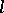 -homomorphism of an
-homomorphism of an 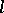 -group
-group 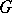 into an
into an  -group
-group 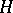 is a homomorphism
is a homomorphism 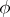 of the group
of the group  into the group
into the group  such that
such that
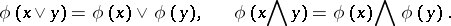 |
The kernels of  -homomorphisms are precisely the
-homomorphisms are precisely the 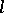 -ideals of
-ideals of 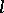 -groups. If
-groups. If  is an
is an  -group and
-group and 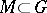 , then the set
, then the set 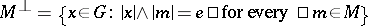 is a convex
is a convex 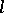 -subgroup in
-subgroup in 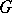 (cf. Convex subgroup).
(cf. Convex subgroup).
The group 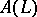 of one-to-one order-preserving mappings of a totally ordered set
of one-to-one order-preserving mappings of a totally ordered set 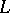 onto itself is an
onto itself is an 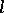 -group (if for
-group (if for 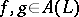 one assumes that
one assumes that 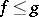 if and only if
if and only if 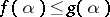 for all
for all 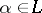 ). Every
). Every 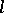 -group is
-group is  -isomorphic to an
-isomorphic to an 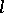 -subgroup of the lattice-ordered group
-subgroup of the lattice-ordered group 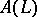 for a suitable set
for a suitable set 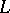 .
.
The class of all lattice-ordered groups is a variety of signature 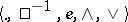 (cf. Variety of groups). Its most important subvariety is the class of lattice-ordered groups that can be approximated by totally ordered groups (the class of representable
(cf. Variety of groups). Its most important subvariety is the class of lattice-ordered groups that can be approximated by totally ordered groups (the class of representable  -groups, cf. also Totally ordered group).
-groups, cf. also Totally ordered group).
References
| [1] | G. Birkhoff, "Lattice theory" , Colloq. Publ. , 25 , Amer. Math. Soc. (1973) |
| [2] | L. Fuchs, "Partially ordered algebraic systems" , Pergamon (1963) |
Comments
References
| [a1] | M. Anderson, T. Feil, "Lattice-ordered groups. An introduction" , Reidel (1988) |
| [a2] | A.M.W. Glass (ed.) W.Ch. Holland (ed.) , Lattice-ordered groups. Advances and techniques , Kluwer (1989) |
| [a3] | J. Martinez (ed.) , Ordered algebraic structures , Kluwer (1989) |
Lattice-ordered group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lattice-ordered_group&oldid=15070