Large sieve

A method developed by Yu.B. Linnik in 1941 which permits one to sift out in sequences of increasing numbers the residues to be discarded. Its essence may be explained as follows. Consider a given sequence of positive integers not larger than , a prime number and a residue , . Let

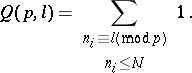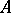It follows from statistical considerations, which may be rigorously proved with the aid of the fundamental idea of the circle method, that for almost-all , and hence also for almost-all . Let be the number of such 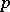's, and let 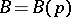be the number of corresponding 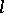's. Linnik showed that

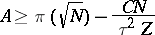and

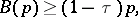where 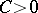is a constant and 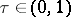, and deduced the theorem: The number of primes on the segment 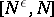to which Vinogradov's hypothesis on the least square non-residue (cf. Vinogradov hypotheses) does not apply can only be finite (depending on ).

There exists an improved method of the large sieve in which the average values of 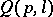are estimated. The best result is due to E. Bombieri (1965):

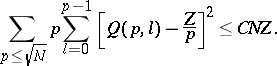The method of the large sieve made its most important contribution to modern analytic number theory in the context of the density method; this resulted in a proof of the Vinogradov–Bombieri theorem (1965) — the averaged asymptotic law of prime numbers in progressions. This and other similar theorems about the average found extensive application in the solution of several familiar problems in number theory, replacing the generalized Riemann hypothesis (cf. Riemann hypothesis, generalized) in many cases.

References

[1]	K. Prachar, "Primzahlverteilung" , Springer (1957)
[2]	H. Davenport, "Multiplicative number theory" , Springer (1980)
[3]	H. Halberstam, H.-E. Richert, "Sieve methods" , Acad. Press (1974)

References

[a1]	E. Bombieri, "Le grand crible dans la théorie analytique des nombres" Astérisque , 18 (1974)