Laplace theorem
Laplace's theorem on determinants. See Cofactor.
Laplace's theorem on the approximation of the binomial distribution by the normal distribution. This is the first version of the central limit theorem of probability theory: If  is the number of "successes" in
is the number of "successes" in  Bernoulli trials with probability of success
Bernoulli trials with probability of success  ,
,  , then, as
, then, as  , for any real numbers
, for any real numbers  and
and  (
( ) one has
) one has
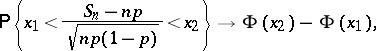 | (*) |
where
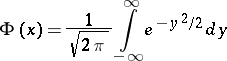 |
is the distribution function of the standard normal law.
The local Laplace theorem has independent significance: For the probability
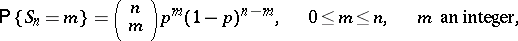 |
one has
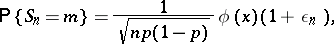 |
where
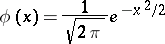 |
is the density of the standard normal distribution and 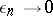 as
as 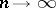 uniformly for all
uniformly for all 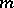 for which
for which  belongs to some finite interval.
belongs to some finite interval.
In its general form the theorem was proved by P.S. Laplace [1]. The special case  of the Laplace theorem was studied by A. de Moivre [2], and therefore the Laplace theorem is sometimes called the de Moivre–Laplace theorem.
of the Laplace theorem was studied by A. de Moivre [2], and therefore the Laplace theorem is sometimes called the de Moivre–Laplace theorem.
For practical applications the Laplace theorem is important in order to obtain an idea of the errors that arise in the use of approximate formulas. In the more precise (by comparison with [1]) asymptotic formula
 |
the remainder term  has order
has order 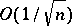 uniformly for all real
uniformly for all real 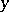 . For uniform approximation of the binomial distribution by means of the normal distribution the formula of Ya. Uspenskii (1937) is more useful: If
. For uniform approximation of the binomial distribution by means of the normal distribution the formula of Ya. Uspenskii (1937) is more useful: If 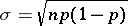 , then for any
, then for any 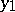 and
and 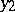 ,
,
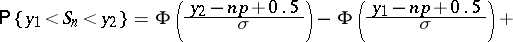 |
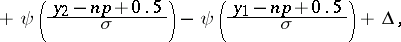 |
where
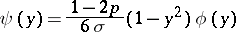 |
and for 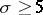 ,
,
 |
To improve the relative accuracy of the approximation S.N. Bernstein [S.N. Bernshtein] (1943) and W. Feller (1945) suggested other formulas.
References
| [1] | P.S. Laplace, "Théorie analytique des probabilités" , Paris (1812) |
| [2] | A. de Moivre, "Miscellanea analytica de seriebus et quadraturis" , London (1730) |
| [3] | Yu.V. [Yu.V. Prokhorov] Prohorov, Yu.A. Rozanov, "Probability theory, basic concepts. Limit theorems, random processes" , Springer (1969) (Translated from Russian) |
| [4] | W. Feller, "On the normal approximation to the binomial distribution" Ann. Math. Statist. , 16 (1945) pp. 319–329 |
| [5] | W. Feller, "An introduction to probability theory and its applications" , 1 , Wiley (1968) |
Comments
For a more detailed and more general discussion of approximation by the normal distribution see [a1].
References
| [a1] | V.V. Petrov, "Sums of independent random variables" , Springer (1975) (Translated from Russian) |
Laplace theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Laplace_theorem&oldid=12520