Laplace equation
A homogeneous partial differential equation of the form
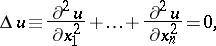 | (1) |
where 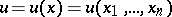 is a function of
is a function of  real variables. The left-hand side of the Laplace equation is called the Laplace operator acting on
real variables. The left-hand side of the Laplace equation is called the Laplace operator acting on  . Regular solutions of the Laplace equation of class
. Regular solutions of the Laplace equation of class 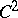 in some domain
in some domain 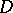 of the Euclidean space
of the Euclidean space 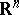 ,
, 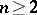 , that is, solutions that have continuous partial derivatives up to the second order in
, that is, solutions that have continuous partial derivatives up to the second order in 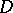 , are called harmonic functions (cf. Harmonic function) in
, are called harmonic functions (cf. Harmonic function) in 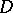 . The Laplace equation is the main representative of second-order partial differential equations of elliptic type, for which fundamental methods of solution of boundary value problems for elliptic equations (cf. Boundary value problem, elliptic equations) have been and are being developed.
. The Laplace equation is the main representative of second-order partial differential equations of elliptic type, for which fundamental methods of solution of boundary value problems for elliptic equations (cf. Boundary value problem, elliptic equations) have been and are being developed.
Let  be a potential vector field in
be a potential vector field in 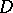 , that is,
, that is, 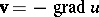 , where
, where 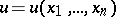 is the potential. Since
is the potential. Since
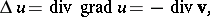 |
the physical meaning of the Laplace equation is that it is satisfied by the potential of any such field in source-free domains 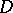 . For example, the Laplace equation is satisfied by the gravitational potential of the gravity force in domains free from attracting masses, the potential of an electrostatic field in a domain free from charges, etc. Thus, the Laplace equation expresses the conservation law for a potential field. From this point of view the form (1) of the Laplace equation is obtained by choosing a rectangular Cartesian coordinate system; in other coordinate systems the Laplace operator and the Laplace equation take a different form. In the presence of sources of the field there appears a function proportional to the density of the sources on the right-hand side of (1), and the Laplace equation becomes the Poisson equation. The Laplace equation also arises in many other problems in mathematical physics in which stationary fields are considered, for example, in the study of a stationary temperature distribution, in problems of static elasticity theory, etc.
. For example, the Laplace equation is satisfied by the gravitational potential of the gravity force in domains free from attracting masses, the potential of an electrostatic field in a domain free from charges, etc. Thus, the Laplace equation expresses the conservation law for a potential field. From this point of view the form (1) of the Laplace equation is obtained by choosing a rectangular Cartesian coordinate system; in other coordinate systems the Laplace operator and the Laplace equation take a different form. In the presence of sources of the field there appears a function proportional to the density of the sources on the right-hand side of (1), and the Laplace equation becomes the Poisson equation. The Laplace equation also arises in many other problems in mathematical physics in which stationary fields are considered, for example, in the study of a stationary temperature distribution, in problems of static elasticity theory, etc.
The following boundary value problems of potential theory are fundamental for the Laplace equation: 1) the Dirichlet problem, or first boundary value problem, in which one looks for a harmonic function that takes given continuous values on the boundary 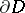 of the domain; 2) the Neumann problem, or second boundary value problem, in which one looks for a harmonic function
of the domain; 2) the Neumann problem, or second boundary value problem, in which one looks for a harmonic function  such that its normal derivative
such that its normal derivative 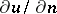 takes given continuous values on
takes given continuous values on 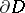 ; and 3) the mixed problem, in which one looks for a harmonic function
; and 3) the mixed problem, in which one looks for a harmonic function  that satisfies a linear relation
that satisfies a linear relation
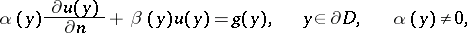 |
on the boundary.
In the case 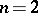 the Laplace equation is closely connected with the theory of analytic functions of a complex variable
the Laplace equation is closely connected with the theory of analytic functions of a complex variable 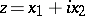 , which are characterized by the fact that their real and imaginary parts are conjugate harmonic functions.
, which are characterized by the fact that their real and imaginary parts are conjugate harmonic functions.
The Laplace equation occurs in papers of L. Euler and J. d'Alembert (see [1], [2]) in connection with problems of hydromechanics and the first studies of functions of a complex variable. However, it became widely known after the appearance of the papers of P.S. Laplace (see [3], [4]) on the theory of the gravitational potential and celestial mechanics.
Equation (1) is sometimes called the scalar Laplace equation, by contrast with the vector Laplace equation
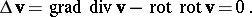 | (2) |
For example, in the case of a vector field 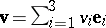 , defined in a rectangular Cartesian coordinate system of
, defined in a rectangular Cartesian coordinate system of 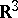 , the vector Laplace equation (2) is equivalent to three scalar Laplace equations
, the vector Laplace equation (2) is equivalent to three scalar Laplace equations 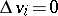 for each of the components
for each of the components 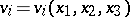 ,
, 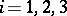 . In other coordinate systems the vector Laplace equation is equivalent to a system of three partial differential equations of the second order for the components of the vector field
. In other coordinate systems the vector Laplace equation is equivalent to a system of three partial differential equations of the second order for the components of the vector field  , obtained from (2) after carrying out the operations of vector analysis in the corresponding coordinates (see [7]).
, obtained from (2) after carrying out the operations of vector analysis in the corresponding coordinates (see [7]).
References
| [1] | L. Euler, Novi Commentarii Acad. Sci. Petropolitanae , 6 (1761) |
| [2] | J. d'Alembert, "Opuscules mathématiques" , 1 , Paris (1761) |
| [3] | P.S. Laplace, Hist. Acad. Sci. Paris (1782) (1785) |
| [4] | P.S. Laplace, "Celestial mechanics" , 2 , Chelsea, reprint (1966) (Translated from French) |
| [5] | V.S. Vladimirov, "Equations of mathematical physics" , MIR (1984) (Translated from Russian) |
| [6] | A.I. Markushevich, "Theory of functions of a complex variable" , 2 , Chelsea (1977) (Translated from Russian) |
| [7] | P.M. Morse, H. Feshbach, "Methods of theoretical physics" , 2 , McGraw-Hill (1953) |
Comments
The solutions of the Laplace equation in a domain 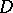 have remarkable properties. For instance, they are analytic in
have remarkable properties. For instance, they are analytic in 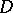 ; their derivatives of any order can be estimated in terms of the distance from the boundary of
; their derivatives of any order can be estimated in terms of the distance from the boundary of 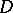 ; they satisfy the mean-value theorem, the weak and strong maximum principle, Hopf's lemma about the behaviour in the vicinity of absolute extrema at boundary points, the Harnack inequality, Harnack's theorem (cf. Harnack theorem), the Dirichlet variational principle (cf. Dirichlet variational problem), etc.
; they satisfy the mean-value theorem, the weak and strong maximum principle, Hopf's lemma about the behaviour in the vicinity of absolute extrema at boundary points, the Harnack inequality, Harnack's theorem (cf. Harnack theorem), the Dirichlet variational principle (cf. Dirichlet variational problem), etc.
The representation of a conservative field as the gradient of a function is introduced in [a2]. In [3] the Laplace equation is given in polar coordinates. The Laplace equation in rectangular coordinates is introduced in [a3]. [a1] contains a systematic treatment of the Laplace equation in curvilinear coordinates.
References
| [a1] | M. Bôcher, "Ueber die Reihenentwicklungen der Potentialtheorie" , Teubner (1894) |
| [a2] | J.L. Lagrange, "Sur l'équation séculaire de la lune" Mém. Acad. Roy. Sci. Paris (1773) |
| [a3] | P.S. Laplace, "Mémoire sur la théorie de l'anneau de Saturne" Hist. Acad. Sci. Paris (1787) |
| [a4] | S. Lang, "Complex analysis" , Springer (1985) |
| [a5] | D. Gilbarg, N.S. Trudinger, "Elliptic partial differential equations of second order" , Springer (1983) |
| [a6] | I.G. Petrovskii, "Partial differential equations" , Saunders (1967) (Translated from Russian) |
| [a7] | R. Courant, D. Hilbert, "Methods of mathematical physics. Partial differential equations" , 2 , Interscience (1965) (Translated from German) |
| [a8] | A.N. [A.N. Tikhonov] Tichonoff, A.A. Samarskii, "Differentialgleichungen der mathematischen Physik" , Deutsch. Verlag Wissenschaft. (1959) (Translated from Russian) |
Laplace equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Laplace_equation&oldid=13017