Laplace distribution
A continuous probability distribution with density
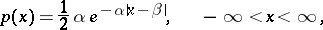 |
where  ,
,  , is a shift parameter and
, is a shift parameter and  is a scale parameter. The density of the Laplace distribution is symmetric about the point
is a scale parameter. The density of the Laplace distribution is symmetric about the point  , and the derivative of the density has a discontinuity at
, and the derivative of the density has a discontinuity at  . The characteristic function of the Laplace distribution with parameters
. The characteristic function of the Laplace distribution with parameters  and
and  is
is
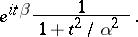 |
The Laplace distribution has finite moments of any order. In particular, its mathematical expectation is 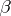 and its variance (cf. Dispersion) is
and its variance (cf. Dispersion) is 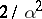 .
.
The Laplace distribution was first introduced by P. Laplace [1] and is often called the "first law of Laplacefirst law of Laplace" , in contrast to the "second law of Laplacesecond law of Laplace" , as the normal distribution is sometimes called. The Laplace distribution is also called the two-sided exponential distribution, on account of the fact that the Laplace distribution coincides with the distribution of the random variable
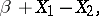 |
where  and
and 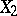 are independent random variables that have the same exponential distribution with density
are independent random variables that have the same exponential distribution with density  ,
, 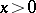 . The Laplace distribution with density
. The Laplace distribution with density  and the Cauchy distribution with density
and the Cauchy distribution with density  are related in the following way:
are related in the following way:
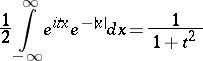 |
and
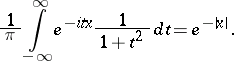 |
References
| [1] | P.S. Laplace, "Théorie analytique des probabilités", Paris (1812) |
| [2] | W. Feller, "An introduction to probability theory and its applications", 2, Wiley (1971) |
Comments
References
| [a1] | E. Lukacs, "Characteristic functions" , Griffin (1970) |
Laplace distribution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Laplace_distribution&oldid=25936