Langevin equation
In 1908 P. Langevin [a1] proposed the following equation to describe the natural phenomenon of Brownian motion (the irregular vibrations of small dust particles suspended in a liquid):
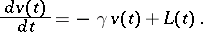 | (a1) |
Here 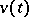 denotes the velocity at time
denotes the velocity at time 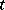 along one of the coordinate axes of the Brownian particle,
along one of the coordinate axes of the Brownian particle, 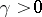 is a friction coefficient due to the viscosity of the liquid, and
is a friction coefficient due to the viscosity of the liquid, and  is a postulated "Langevin forceLangevin force" , standing for the pressure fluctuations due to thermal motion of the molecules comprising the liquid. This Langevin force was supposed to have the properties
is a postulated "Langevin forceLangevin force" , standing for the pressure fluctuations due to thermal motion of the molecules comprising the liquid. This Langevin force was supposed to have the properties
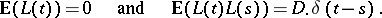 |
The Langevin equation (a1) leads to the following diffusion (or "Fokker–Planck" ) equation (cf. Diffusion equation) for the probability density on the velocity axis:
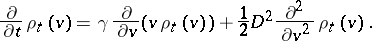 | (a2) |
The equations (a1) and (a2) provided a conceptual and quantitative improvement on the description of the phenomenon of Brownian motion given by A. Einstein in 1905. The quantitative understanding of Brownian motion played a large role in the acceptance of the theory of molecules by the scientific community. The numerical relation between the two observable constants 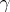 and
and 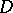 , namely
, namely 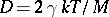 (where
(where 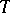 is the temperature and
is the temperature and  the particle's mass), gave the first estimate of Boltzmann's constant
the particle's mass), gave the first estimate of Boltzmann's constant  , and thereby of Avogadro's number.
, and thereby of Avogadro's number.
The Langevin equation may be considered as the first stochastic differential equation. Today it would be written as
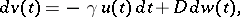 |
where 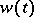 is the Wiener process (confusingly called "Brownian motion" as well). The solution of the Langevin equation is a Markov process, first described by G.E. Uhlenbeck and L.S. Ornstein in 1930 [a2] (cf. also Ornstein–Uhlenbeck process).
is the Wiener process (confusingly called "Brownian motion" as well). The solution of the Langevin equation is a Markov process, first described by G.E. Uhlenbeck and L.S. Ornstein in 1930 [a2] (cf. also Ornstein–Uhlenbeck process).
The Langevin equation is a heuristic equation. The program to give it a solid foundation in Hamiltonian mechanics has not yet fully been carried through. Considerable progress was made by G.W. Ford, M. Kac and P. Mazur [a3], who showed that the process of Uhlenbeck and Ornstein can be realized by coupling the Brownian particle in a specific way to an infinite number of harmonic oscillators put in a state of thermal equilibrium.
In more recent years, quantum mechanical versions of the Langevin equation have been considered. They can be subdivided into two classes: those which yield Markov processes and those which satisfy a condition of thermal equilibrium. The former are known as "quantum stochastic differential equations" [a4], the latter are named "quantum Langevin equations" [a5].
References
| [a1] | P. Langevin, "Sur la théorie de mouvement Brownien" C.R. Acad. Sci. Paris , 146 (1908) pp. 530–533 |
| [a2] | G.E. Uhlenbeck, L.S. Ornstein, "On the theory of Brownian motion" Phys. Rev. , 36 (1930) pp. 823–841 |
| [a3] | G.W. Ford, M. Kac, P. Mazur, "Statistical mechanics of assemblies of coupled oscillators" J. Math. Phys. , 6 (1965) pp. 504–515 |
| [a4] | C. Barnett, R.F. Streater, I.F. Wilde, "Quasi-free quantum stochastic integrals for the CAR and CCR" J. Funct. Anal. , 52 (1983) pp. 19–47 |
| [a5] | R.L. Hudson, K.R. Parthasarathy, "Quantum Itô's formula and stochastic evolutions" Commun. Math. Phys. , 93 (1984) pp. 301–323 |
Langevin equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Langevin_equation&oldid=16399