Lambert summation method
From Encyclopedia of Mathematics
The printable version is no longer supported and may have rendering errors. Please update your browser bookmarks and please use the default browser print function instead.
A method for summing series of numbers. The series
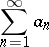 |
is summable by Lambert's method to the number 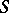 if
if
 |
where
 |
and if the series on the right-hand side converges. The method was proposed by J.H. Lambert [1]. The summability of a series by the Cesàro summation method 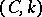 for some
for some 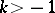 (cf. Cesàro summation methods) to the sum
(cf. Cesàro summation methods) to the sum 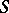 implies its summability by the Lambert method to the same sum, and if the series is summable by the Lambert method to the sum
implies its summability by the Lambert method to the same sum, and if the series is summable by the Lambert method to the sum 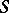 , then it is also summable by the Abel summation method to the same sum. Lambert's summation method is regular (see Regular summation methods).
, then it is also summable by the Abel summation method to the same sum. Lambert's summation method is regular (see Regular summation methods).
References
| [1] | J.H. Lambert, "Anlage zur Architektonik" , 2 , Riga (1771) |
| [2] | G.H. Hardy, "Divergent series" , Clarendon Press (1949) |
How to Cite This Entry:
Lambert summation method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lambert_summation_method&oldid=14975
Lambert summation method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lambert_summation_method&oldid=14975
This article was adapted from an original article by I.I. Volkov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article