Lambert series
The series of functions
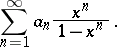 | (1) |
It was considered by J.H. Lambert (see [1]) in connection with questions of convergence of power series. If the series
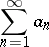 |
converges, then the Lambert series converges for all values of  except
except 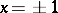 ; otherwise it converges for those values of
; otherwise it converges for those values of  for which the series
for which the series
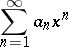 |
converges. The Lambert series is used in certain problems of number theory. Thus, for 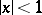 the sum
the sum 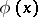 of the series (1) can be represented as a power series:
of the series (1) can be represented as a power series:
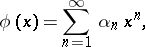 | (2) |
where
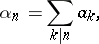 |
and the summation is over all divisors 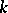 of
of  . In particular, if
. In particular, if 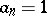 , then
, then 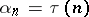 , the number of divisors of
, the number of divisors of  ; if
; if 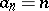 , then
, then 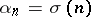 , the sum of the divisors of
, the sum of the divisors of  . The behaviour of
. The behaviour of 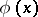 (with suitable
(with suitable 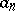 ) as
) as 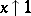 is used, for example (see [3]), in the problem of Hardy and Ramanujan on obtaining an asymptotic formula for the number of "unbounded partitions" of a natural number.
is used, for example (see [3]), in the problem of Hardy and Ramanujan on obtaining an asymptotic formula for the number of "unbounded partitions" of a natural number.
References
| [1] | J.H. Lambert, "Opera Mathematica" , 1–2 , O. Füssli (1946–1948) |
| [2] | G.M. Fichtenholz, "Differential und Integralrechnung" , 2 , Deutsch. Verlag Wissenschaft. (1964) |
| [3] | A.G. Postnikov, "Introduction to analytic number theory" , Moscow (1971) (In Russian) |
Comments
Lambert series also occur in the expansion of Eisenstein series, a particular kind of modular form. See [a1].
References
| [a1] | T.M. Apostol, "Modular forms and Dirichlet series in analysis" , Springer (1976) |
| [a2] | H. Rademacher, "Topics in analytic number theory" , Springer (1973) |
| [a3] | K. Knopp, "Theorie und Anwendung der unendlichen Reihen" , Springer (1964) (English translation: Blackie, 1951 & Dover, reprint, 1990) |
Lambert series. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lambert_series&oldid=13504