of an orthogonal curvilinear coordinate system  in space
in space
The quantities
The Lamé coefficients in the plane are defined similarly. In terms of the Lamé coefficients in the coordinates  one can express the element of arc length:
one can express the element of arc length:
the element of surface area:
and the volume element:
The Lamé coefficients occur in the expressions for the operations of vector analysis in the coordinates  :
:
For the Lamé coefficients of various orthogonal curvilinear coordinates see the corresponding articles on those coordinates.
Lamé coefficients were introduced by G. Lamé [1].
References
| [1] | G. Lamé, "Leçons sur les coordonnées curvilignes et leurs diverses applications" , Paris (1859) |
| [2] | G.F. Laptev, "Elements of vector calculus" , Moscow (1975) (In Russian) |
| [3] | P.M. Morse, H. Feshbach, "Methods of theoretical physics" , 1 , McGraw-Hill (1953) |
The name "Lamé coefficients" for the quantities 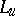 ,
, 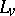 ,
, 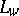 is not often used in the Western literature. Instead one finds "scale factors of an orthogonal curvilinear coordinate systemscale factors" [3] or "metric coefficients of an orthogonal curvilinear coordinate systemmetric coefficients" [a1]. The latter terminology of course derives from the fact that the original Riemannian metric
is not often used in the Western literature. Instead one finds "scale factors of an orthogonal curvilinear coordinate systemscale factors" [3] or "metric coefficients of an orthogonal curvilinear coordinate systemmetric coefficients" [a1]. The latter terminology of course derives from the fact that the original Riemannian metric 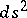 with respect to the new orthogonal curvilinear system of coordinates
with respect to the new orthogonal curvilinear system of coordinates 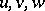 takes the form
takes the form
Thus the squares of the 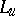 ,
, 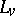 ,
, 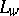 are the diagonal components of the standard metric tensor on
are the diagonal components of the standard metric tensor on 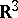 expressed in terms of
expressed in terms of 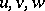 . The other components are zero because
. The other components are zero because 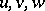 is an orthogonal curvilinear coordinate system.
is an orthogonal curvilinear coordinate system.
References
| [a1] | I.S. [I.S. Sokolnikov] Sokolnikoff, R.M. Redheffer, "Mathematics of physics and engineering" , McGraw-Hill (1958) |
| [a2] | H.F. Davis, A.D. Snider, "Introduction to vector analysis" , Allyn & Bacon (1979) |
How to Cite This Entry:
Lamé coefficients. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lam%C3%A9_coefficients&oldid=23360
This article was adapted from an original article by V.I. Bityutskov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article in space
in space
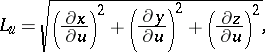

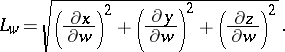
 one can express the element of arc length:
one can express the element of arc length:
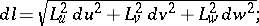
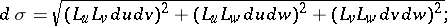
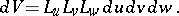
 :
:
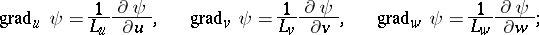
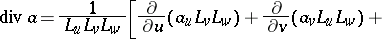

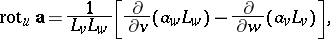
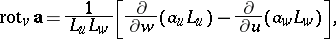
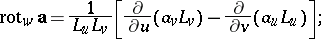
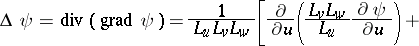
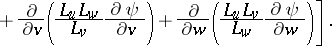
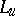 ,
, 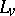 ,
, 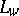 is not often used in the Western literature. Instead one finds "scale factors of an orthogonal curvilinear coordinate systemscale factors" [3] or "metric coefficients of an orthogonal curvilinear coordinate systemmetric coefficients" [a1]. The latter terminology of course derives from the fact that the original Riemannian metric
is not often used in the Western literature. Instead one finds "scale factors of an orthogonal curvilinear coordinate systemscale factors" [3] or "metric coefficients of an orthogonal curvilinear coordinate systemmetric coefficients" [a1]. The latter terminology of course derives from the fact that the original Riemannian metric 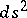 with respect to the new orthogonal curvilinear system of coordinates
with respect to the new orthogonal curvilinear system of coordinates 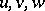 takes the form
takes the form
 ,
,  ,
,  are the diagonal components of the standard metric tensor on
are the diagonal components of the standard metric tensor on 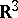 expressed in terms of
expressed in terms of 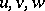 . The other components are zero because
. The other components are zero because 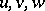 is an orthogonal curvilinear coordinate system.
is an orthogonal curvilinear coordinate system.