L-matrix
Matrices playing a central role in the study of qualitative economics and first defined by P.A. Samuelson [a6]. A real 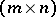 -matrix
-matrix 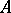 is an
is an  -matrix provided every matrix with the same sign pattern as
-matrix provided every matrix with the same sign pattern as 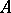 has linearly independent rows. For example,
has linearly independent rows. For example,
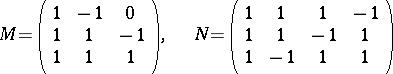 |
are 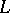 -matrices. A linear system of equations,
-matrices. A linear system of equations, 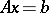 , is called sign-solvable provided the signs of the entries in any solution can be determined knowing only the signs of the entries in
, is called sign-solvable provided the signs of the entries in any solution can be determined knowing only the signs of the entries in 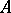 and
and 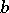 . If the linear system
. If the linear system 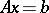 is sign-solvable, then
is sign-solvable, then 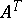 is an
is an 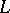 -matrix. General references for this area include [a1], [a3] and [a4].
-matrix. General references for this area include [a1], [a3] and [a4].
The study of 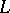 -matrices has included characterizations of structural properties, classification of subclasses as well as interrelationships with other discrete structures. For example, two subclasses of
-matrices has included characterizations of structural properties, classification of subclasses as well as interrelationships with other discrete structures. For example, two subclasses of 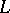 -matrices which arise are that of the barely
-matrices which arise are that of the barely 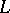 -matrices and the totally
-matrices and the totally 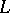 -matrices.
-matrices.
An 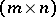 -matrix
-matrix  is a barely
is a barely 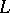 -matrix provided that
-matrix provided that 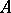 is an
is an 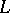 -matrix but if any column of it is deleted, the resulting matrix is not an
-matrix but if any column of it is deleted, the resulting matrix is not an 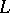 -matrix.
-matrix.
An 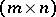 -matrix
-matrix 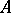 is a totally
is a totally 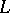 -matrix provided that each
-matrix provided that each 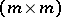 -submatrix of
-submatrix of 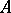 is an
is an 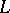 -matrix.
-matrix.
The two matrices  and
and 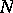 above are examples of barely
above are examples of barely 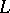 -matrices. The matrix
-matrices. The matrix 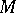 is also a totally
is also a totally 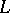 -matrix but
-matrix but 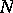 is not since its
is not since its  -submatrix made up of the first three columns is not an
-submatrix made up of the first three columns is not an  -matrix. The matrix
-matrix. The matrix
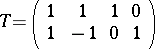 |
is a 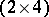 totally
totally  -matrix.
-matrix.
The property of being a barely  -matrix, or a totally
-matrix, or a totally  -matrix, imposes restrictions on the number of columns. If
-matrix, imposes restrictions on the number of columns. If 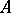 is an
is an 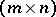 barely
barely 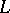 -matrix, then the number of columns is at most
-matrix, then the number of columns is at most 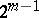 ; further, if
; further, if 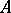 has only non-negative entries, then the number of columns is at most
has only non-negative entries, then the number of columns is at most
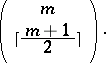 |
If  is an
is an 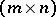 totally
totally 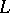 -matrix, then the number of columns is at most
-matrix, then the number of columns is at most 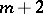 . It has been shown that the set of all
. It has been shown that the set of all 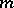 by
by  totally
totally 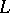 -matrices can be obtained from the matrix
-matrices can be obtained from the matrix 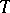 above by performing certain extension operations on
above by performing certain extension operations on 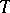 successively [a2].
successively [a2].
An important subclass of the 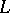 -matrices for which there exist a great deal of literature is that of the square
-matrices for which there exist a great deal of literature is that of the square 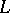 -matrices, which are also called sign-non-singular matrices.
-matrices, which are also called sign-non-singular matrices.
References
| [a1] | L. Bassett, J. Maybee, J. Quirk, "Qualitative economics and the scope of the correspondence principle" Econometrica , 36 (1968) pp. 544–563 |
| [a2] | R.A. Brualdi, K.L. Chavey, B.L. Shader, "Rectangular L-matrices" Linear Algebra Appl. , 196 (1994) pp. 37–61 |
| [a3] | R.A. Brualdi, B.L. Shader, "Matrices of sign solvable systems" , Tracts in Math. , 116 , Cambridge Univ. Press (1995) |
| [a4] | V. Klee, R. Ladner, R. Manber, "Sign-solvability revisited" Linear Algebra Appl. , 59 (1984) pp. 131–157 |
| [a5] | R. Manber, "Graph-theoretical approach to qualitative solvability of linear systems" Linear Algebra Appl. , 48 (1982) pp. 131–157 |
| [a6] | P.A. Samuelson, "Foundations of economic analysis" , Economic Studies , 80 , Harvard Univ. Press (1947) |
L-matrix. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=L-matrix&oldid=13301