L-group
lattice-ordered group
A partially ordered group 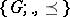 (cf.
(cf.  -group) such that
-group) such that 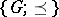 is a lattice (cf. also Lattice-ordered group). It is useful to consider the
is a lattice (cf. also Lattice-ordered group). It is useful to consider the 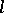 -group
-group 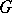 as an algebraic system
as an algebraic system 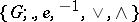 , where
, where 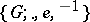 is a group with identity element
is a group with identity element  , and
, and 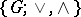 is a lattice with join and meet operations
is a lattice with join and meet operations 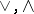 in the lattice
in the lattice 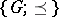 . The following identities hold in any
. The following identities hold in any 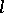 -group:
-group:
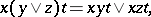 |
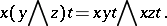 |
The lattice of an 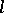 -group is distributive (cf. Distributive lattice). The class of all
-group is distributive (cf. Distributive lattice). The class of all 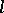 -groups is a variety of signature
-groups is a variety of signature 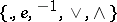 (cf.
(cf. 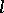 -variety); it is locally closed, and closed under taking direct and Cartesian products,
-variety); it is locally closed, and closed under taking direct and Cartesian products, 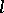 -subgroups (i.e., subgroups that are sublattices), and
-subgroups (i.e., subgroups that are sublattices), and 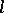 -homomorphisms (i.e., homomorphisms that preserve the group operation
-homomorphisms (i.e., homomorphisms that preserve the group operation  and the lattice operations
and the lattice operations 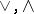 ).
).
The most important examples of 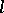 -groups are: 1) the additive group
-groups are: 1) the additive group 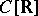 of the set of real-valued continuous functions defined on the real number set
of the set of real-valued continuous functions defined on the real number set 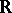 , with the order:
, with the order: 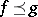 , for
, for 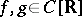 , if and only if
, if and only if 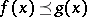 for all
for all 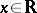 ; and 2) the automorphism group
; and 2) the automorphism group 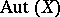 of a totally ordered set
of a totally ordered set 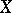 with order:
with order: 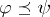 , for
, for 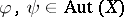 , if and only if
, if and only if 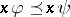 for all
for all 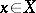 .
.
The theory of 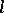 -groups is used in the study of the structure of ordered vector spaces, function spaces and infinite groups, in particular for the groups
-groups is used in the study of the structure of ordered vector spaces, function spaces and infinite groups, in particular for the groups 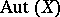 .
.
The most important fact of the theory of 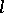 -groups is that every
-groups is that every 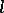 -group is
-group is 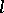 -isomorphic to some
-isomorphic to some 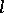 -subgroup of the
-subgroup of the 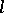 -group
-group  for a suitable totally ordered
for a suitable totally ordered 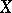 . Using this theorem, it can be proved that every
. Using this theorem, it can be proved that every 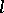 -group is imbeddable in a divisible
-group is imbeddable in a divisible 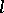 -group as well as in a simple group. The class of groups that may be endowed with the structure of an
-group as well as in a simple group. The class of groups that may be endowed with the structure of an 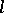 -group is large. E.g., it contains the classes of Abelian torsion-free groups, locally nilpotent torsion-free groups, and many others. There are torsion-free groups that cannot be imbedded in any
-group is large. E.g., it contains the classes of Abelian torsion-free groups, locally nilpotent torsion-free groups, and many others. There are torsion-free groups that cannot be imbedded in any 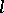 -group.
-group.
Every 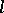 -group is a torsion-free group and has a decomposition property: if
-group is a torsion-free group and has a decomposition property: if 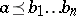 for positive elements
for positive elements  , then
, then 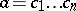 , where
, where 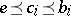 .
.
Let 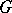 be an
be an 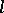 -group and put
-group and put 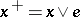 ,
, 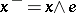 ,
, 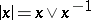 for
for 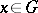 . Then
. Then
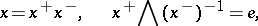 |
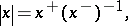 |
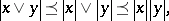 |
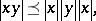 |
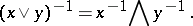 |
Elements 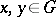 are called orthogonal if
are called orthogonal if 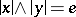 . Orthogonal elements commute.
. Orthogonal elements commute.
An 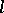 -group may be described by its positive cone
-group may be described by its positive cone 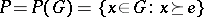 , for which the following properties hold:
, for which the following properties hold:
1) 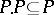 ;
;
2) 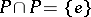 ;
;
3) 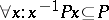 ;
;
4) 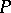 is a lattice respect with the partial order induced from
is a lattice respect with the partial order induced from 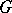 . If, in a group
. If, in a group 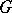 , a set
, a set 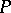 with the properties 1)–4) can be found, then it is possible to turn
with the properties 1)–4) can be found, then it is possible to turn 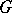 in an
in an 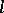 -group by setting
-group by setting 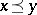 if and only if
if and only if 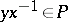 . It is correct to identify the order in an
. It is correct to identify the order in an 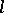 -group with its positive cone. The notation "l-group" is connected with the notation for right-ordered groups (cf.
-group with its positive cone. The notation "l-group" is connected with the notation for right-ordered groups (cf. 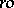 -group). In particular, the positive cone
-group). In particular, the positive cone 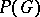 of any
of any 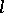 -group
-group 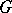 is the intersection of a suitable set of right orders
is the intersection of a suitable set of right orders 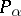 on the group
on the group 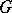 .
.
It is useful to describe the structure of an 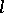 -group in terms of convex
-group in terms of convex 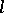 -subgroups (cf. Convex subgroup). A subgroup
-subgroups (cf. Convex subgroup). A subgroup 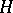 of an
of an 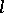 -group
-group 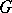 is called a convex subgroup if for all
is called a convex subgroup if for all 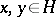 ,
, 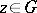 :
:
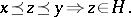 |
The set  of all convex
of all convex  -subgroups of
-subgroups of  is a complete sublattice of the lattice of all subgroups (cf. Complete lattice). A subset
is a complete sublattice of the lattice of all subgroups (cf. Complete lattice). A subset 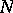 of an
of an 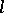 -group
-group 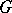 is the kernel of an
is the kernel of an 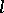 -homomorphism of
-homomorphism of 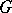 if and only if it is an
if and only if it is an 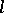 -ideal, i.e., a normal convex
-ideal, i.e., a normal convex 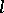 -subgroup of
-subgroup of 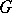 .
.
If 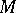 is a subset of an
is a subset of an 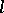 -group
-group 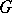 , then the set
, then the set 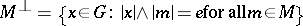 is called a polar. Every polar in a
is called a polar. Every polar in a 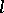 -group
-group 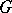 is a convex
is a convex 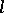 -subgroup of
-subgroup of 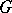 . The following properties hold for polars
. The following properties hold for polars 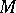 and
and 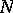 of an
of an 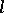 -group
-group 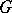 :
:
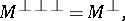 |
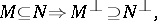 |
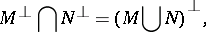 |
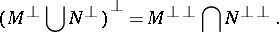 |
The set of all polars of an 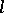 -group
-group 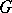 is a Boolean algebra, but not a sublattice of the lattice
is a Boolean algebra, but not a sublattice of the lattice 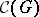 . The properties and the significance of polars are well investigated.
. The properties and the significance of polars are well investigated.
An  -group is an
-group is an 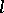 -group with a total order (cf. also Totally ordered group). If an
-group with a total order (cf. also Totally ordered group). If an 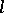 -group
-group  is an
is an 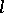 -subgroup of the Cartesian product of totally ordered groups, then
-subgroup of the Cartesian product of totally ordered groups, then  is called a representable group. The class
is called a representable group. The class 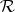 of representable groups has been well investigated. It is the
of representable groups has been well investigated. It is the 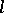 -variety given by the identity
-variety given by the identity 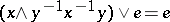 in the variety of all
in the variety of all 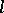 -groups. An
-groups. An 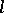 -group is representable if and only if every polar of it is an
-group is representable if and only if every polar of it is an 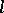 -ideal. The positive cone
-ideal. The positive cone 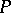 of a representable
of a representable 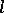 -group
-group 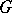 is the intersection of all total orders of
is the intersection of all total orders of 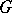 restricted to
restricted to 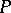 . Every locally nilpotent
. Every locally nilpotent 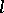 -group is representable.
-group is representable.
An 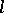 -group
-group 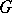 is called Archimedean if the equality
is called Archimedean if the equality 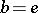 holds for all
holds for all 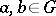 such that
such that 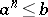 for any integer
for any integer  . Every Archimedean
. Every Archimedean 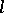 -group is Abelian (cf. Abelian group) and it is an
-group is Abelian (cf. Abelian group) and it is an 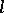 -subgroup of the Cartesian product of copies of the totally ordered additive group of real numbers
-subgroup of the Cartesian product of copies of the totally ordered additive group of real numbers 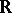 . The class
. The class 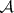 of Archimedean
of Archimedean 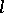 -groups is closed under formation of subgroups, direct and Cartesian products. It is not closed under
-groups is closed under formation of subgroups, direct and Cartesian products. It is not closed under 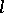 -homomorphisms and is not an
-homomorphisms and is not an 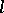 -variety. The
-variety. The 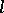 -group
-group 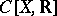 of real-valued functions on a compact topologic space
of real-valued functions on a compact topologic space 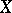 is Archimedean.
is Archimedean.
This article extends and complements the article Lattice-ordered group (Volume 5).
References
| [a1] | L. Fuchs, "Partially ordered algebraic systems" , Pergamon (1963) |
| [a2] | A. Bigard, K. Keimel, S. Wolfenstein, "Groupes et anneaux rétiqulés" , Springer (1977) |
| [a3] | "Lattice-ordered groups: advances and techniques" A.M.W. Glass (ed.) W.Ch. Holland (ed.) , Kluwer Acad. Publ. (1989) |
| [a4] | V.M. Kopytov, N.Ya. Medvedev, "The theory of lattice-ordered groups" , Kluwer Acad. Publ. (1994) (In Russian) |
L-group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=L-group&oldid=17768