Lüroth problem
The problem of characterizing subfields of a field of rational functions.
In 1876 J. Lüroth [1] (see also [2]) proved that any subfield of a field 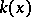 of rational functions in one variable, containing
of rational functions in one variable, containing 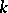 and distinct from
and distinct from 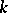 , is isomorphic to the field
, is isomorphic to the field 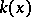 (Lüroth's theorem). The question of whether a similar assertion is true for subfields
(Lüroth's theorem). The question of whether a similar assertion is true for subfields 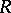 of the field
of the field 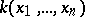 ,
, 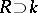 ,
, 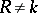 ,
, 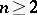 , is known as the Lüroth problem.
, is known as the Lüroth problem.
Let 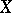 be an algebraic variety that is a model (see Minimal model) of the field
be an algebraic variety that is a model (see Minimal model) of the field  ; then the imbedding
; then the imbedding 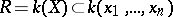 defines a rational mapping
defines a rational mapping 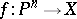 whose image is dense in
whose image is dense in 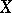 . Varieties for which there is such a mapping of projective space onto them are said to be unirational (cf. Unirational variety). Varieties that are birationally isomorphic to
. Varieties for which there is such a mapping of projective space onto them are said to be unirational (cf. Unirational variety). Varieties that are birationally isomorphic to 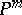 are said to be rational (cf. Rational variety). In geometrical language Lüroth's problem can be stated as follows: Is any unirational variety
are said to be rational (cf. Rational variety). In geometrical language Lüroth's problem can be stated as follows: Is any unirational variety  rational? Without loss of generality one may assume that
rational? Without loss of generality one may assume that 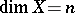 , that is, that
, that is, that 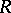 has transcendence degree
has transcendence degree  .
.
In the case 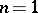 an affirmative solution of Lüroth's problem for any ground field
an affirmative solution of Lüroth's problem for any ground field 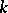 is given by Lüroth's theorem stated above. For
is given by Lüroth's theorem stated above. For 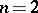 and an algebraically closed field
and an algebraically closed field  of characteristic 0 the problem was solved affirmatively by G. Castelnuovo in 1893. Castelnuovo's rationality criterion implies also an affirmative solution of Lüroth's problem for surfaces
of characteristic 0 the problem was solved affirmatively by G. Castelnuovo in 1893. Castelnuovo's rationality criterion implies also an affirmative solution of Lüroth's problem for surfaces 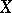 over an algebraically closed field of arbitrary characteristic for which there is a separable mapping
over an algebraically closed field of arbitrary characteristic for which there is a separable mapping 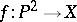 (see [7]). For non-separable mappings
(see [7]). For non-separable mappings 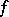 there are examples that give a negative solution of Lüroth's problem for fields of prime characteristic. In the case of an algebraically non-closed field
there are examples that give a negative solution of Lüroth's problem for fields of prime characteristic. In the case of an algebraically non-closed field 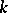 such examples are the minimal cubic surfaces in
such examples are the minimal cubic surfaces in 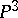 that have
that have 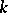 -points.
-points.
For three-dimensional varieties Lüroth's problem has also been solved negatively (see [4], [5], [6]). It has been proved [5] that a three-dimensional cubic hypersurface, which is known to be unirational, is not rational. For the proof a new method was found, based on the comparison of the intermediate Jacobian of the cubic with the Jacobians of curves. It has been proved [4] that smooth three-dimensional quadrics are not rational. In [6], for the construction of counter-examples the Brauer group of the variety (the torsion subgroup of the three-dimensional cohomology group) was used as an invariant. This birational invariant has also been used in the construction of counter-examples in all dimensions 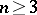 .
.
References
| [1] | J. Lüroth, Math. Ann. , 9 (1876) pp. 163–165 |
| [2] | B.L. van der Waerden, "Algebra" , 1–2 , Springer (1967–1971) (Translated from German) |
| [3] | Yu.I. Manin, "Cubic forms. Algebra, geometry, arithmetic" , North-Holland (1974) (Translated from Russian) |
| [4] | V.A. Iskovskikh, Yu.I. Manin, "Three-dimensional quartics and counterexamples to the Lüroth problem" Math. USSR Sb. , 15 : 1 (1971) pp. 141–166 Mat. Sb. , 86 : 1 (1971) pp. 140–166 |
| [5] | C.H. Clemens, P. Griffiths, "The intermediate Jacobian of the cubic threefold" Ann. of Math. , 95 (1972) pp. 281–356 |
| [6] | M. Artin, D. Mumford, "Some elementary examples of unirational varieties which are not rational" Proc. London Math. Soc. , 25 : 1 (1972) pp. 75–95 |
| [7] | O. Zariski, "The problem of minimal models in the theory of algebraic surfaces" Amer. J. Math. , 80 (1958) pp. 146–184 |
Lüroth problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=L%C3%BCroth_problem&oldid=13635