Löwner equation
A differential equation of the form
 |
where 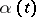 is a real-valued continuous function on the interval
is a real-valued continuous function on the interval 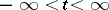 . A generalization of the Löwner equation is the Kufarev–Löwner equation:
. A generalization of the Löwner equation is the Kufarev–Löwner equation:
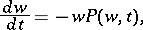 |
where 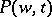 ,
, 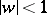 ,
, 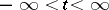 , is a function measurable in
, is a function measurable in 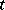 for fixed
for fixed 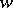 and regular in
and regular in 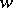 , with positive real part, normalized by the condition
, with positive real part, normalized by the condition 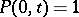 . The Löwner equation and the Kufarev–Löwner equation, which arise in the theory of univalent functions, are the basis of the variation-parametric method of investigating extremal problems on conformal mapping.
. The Löwner equation and the Kufarev–Löwner equation, which arise in the theory of univalent functions, are the basis of the variation-parametric method of investigating extremal problems on conformal mapping.
The solution  ,
, 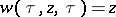 , of the Kufarev–Löwner equation, regarded as a function of the initial value
, of the Kufarev–Löwner equation, regarded as a function of the initial value  , for any
, for any 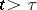 maps the disc
maps the disc 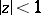 conformally onto a one-sheeted simply-connected domain belonging to the disc
conformally onto a one-sheeted simply-connected domain belonging to the disc 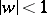 . From the formula
. From the formula
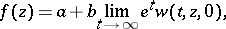 |
by a suitable choice of 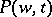 in the Kufarev–Löwner equation and complex constants
in the Kufarev–Löwner equation and complex constants 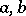 one can obtain an arbitrary regular univalent function in the disc
one can obtain an arbitrary regular univalent function in the disc 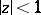 . In this way the Löwner equation generates, in particular, the conformal mappings of the disc onto domains obtained from the whole plane by making a slit along some Jordan arc (see [1]–[4]).
. In this way the Löwner equation generates, in particular, the conformal mappings of the disc onto domains obtained from the whole plane by making a slit along some Jordan arc (see [1]–[4]).
The partial differential equation
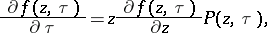 |
which is satisfied by the function
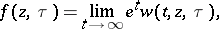 |
is also called the Kufarev–Löwner equation.
The Löwner equation was set up by K. Löwner [1]; the Kufarev–Löwner equation was obtained by P.P. Kufarev (see [5]).
References
| [1] | K. Löwner, "Untersuchungen über schlichte konforme Abbildungen des Einheitskreises, I" Math. Ann. , 89 (1923) pp. 103–121 |
| [2] | P.P. Kufarev, "A theorem on solutions of a differential equation" Uchen. Zap. Tomsk. Gos. Univ. , 5 (1947) pp. 20–21 (In Russian) |
| [3] | C. Pommerenke, "Ueber die Subordination analytischer Funktionen" J. Reine Angew. Math. , 218 (1965) pp. 159–173 |
| [4] | V.Ya. Gutlyanskii, "Parametric representation of univalent functions" Soviet Math. Dokl. , 11 (1970) pp. 1273–1276 Dokl. Akad. Nauk SSSR , 194 : 4 (1970) pp. 750–753 |
| [5] | P.P. Kufarev, "On one-parameter families of analytic functions" Mat. Sb. , 13 (1943) pp. 87–118 (In Russian) |
| [6] | G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian) |
Comments
For more information see also Löwner method.
Löwner equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=L%C3%B6wner_equation&oldid=12765