Lévy canonical representation
A formula for the logarithm 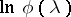 of the characteristic function of an infinitely-divisible distribution:
of the characteristic function of an infinitely-divisible distribution:
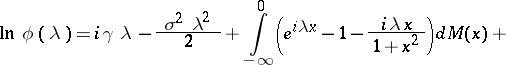 |
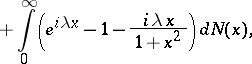 |
where the characteristics of the Lévy canonical representation, 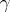 ,
, 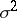 ,
, 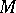 , and
, and 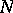 , satisfy the following conditions:
, satisfy the following conditions: 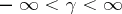 ,
, 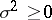 , and
, and 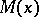 and
and 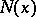 are non-decreasing left-continuous functions on
are non-decreasing left-continuous functions on 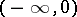 and
and 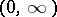 , respectively, such that
, respectively, such that
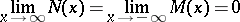 |
and
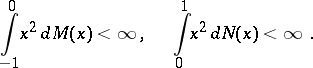 |
To every infinitely-divisible distribution there corresponds a unique system of characteristics 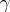 ,
, 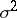 ,
, 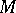 ,
, 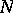 in the Lévy canonical representation, and conversely, under the above conditions on
in the Lévy canonical representation, and conversely, under the above conditions on 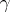 ,
, 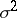 ,
, 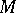 , and
, and 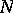 the Lévy canonical representation with respect to such a system determines the logarithm of the characteristic function of some infinitely-divisible distribution.
the Lévy canonical representation with respect to such a system determines the logarithm of the characteristic function of some infinitely-divisible distribution.
Thus, for the normal distribution with mean  and variance
and variance 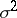 :
:
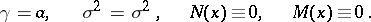 |
For the Poisson distribution with parameter 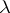 :
:
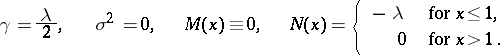 |
To the stable distribution with exponent 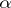 ,
, 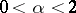 , corresponds the Lévy representation with
, corresponds the Lévy representation with
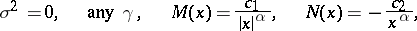 |
where 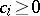 ,
, 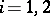 , are constants
, are constants 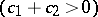 . The Lévy canonical representation of an infinitely-divisible distribution was proposed by P. Lévy in 1934. It is a generalization of a formula found by A.N. Kolmogorov in 1932 for the case when the infinitely-divisible distribution has finite variance. For
. The Lévy canonical representation of an infinitely-divisible distribution was proposed by P. Lévy in 1934. It is a generalization of a formula found by A.N. Kolmogorov in 1932 for the case when the infinitely-divisible distribution has finite variance. For 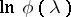 there is a formula equivalent to the Lévy canonical representation, proposed in 1937 by A.Ya. Khinchin and called the Lévy–Khinchin canonical representation. The probabilistic meaning of the functions
there is a formula equivalent to the Lévy canonical representation, proposed in 1937 by A.Ya. Khinchin and called the Lévy–Khinchin canonical representation. The probabilistic meaning of the functions 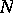 and
and 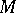 and the range of applicability of the Lévy canonical representation are defined as follows: To every infinitely-divisible distribution function
and the range of applicability of the Lévy canonical representation are defined as follows: To every infinitely-divisible distribution function  corresponds a stochastically-continuous process with stationary independent increments
corresponds a stochastically-continuous process with stationary independent increments
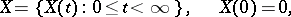 |
such that
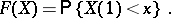 |
In turn, a separable process 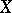 of the type mentioned has with probability 1 sample trajectories without discontinuities of the second kind; hence for
of the type mentioned has with probability 1 sample trajectories without discontinuities of the second kind; hence for 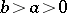 the random variable
the random variable 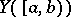 equal to the number of elements in the set
equal to the number of elements in the set
 |
i.e. to the number of jumps with heights in 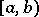 on the interval
on the interval 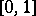 , exists. In this notation, one has for the function
, exists. In this notation, one has for the function 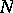 corresponding to
corresponding to 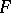 ,
,
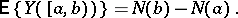 |
A similar relation holds for the function 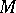 .
.
Many properties of the behaviour of the sample trajectories of a separable process 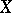 can be expressed in terms of the characteristics of the Lévy canonical representation of the distribution function
can be expressed in terms of the characteristics of the Lévy canonical representation of the distribution function 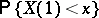 . In particular, if
. In particular, if 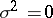 ,
,
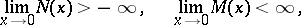 |
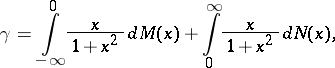 |
then almost-all the sample functions of 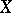 are with probability 1 step functions with finitely many jumps on any finite interval. If
are with probability 1 step functions with finitely many jumps on any finite interval. If 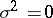 and if
and if
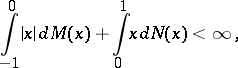 |
then with probability 1 the sample trajectories of 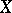 have bounded variation on any finite interval. Directly in terms of the characteristics of the Lévy canonical representation one can calculated the infinitesimal operator corresponding to the process
have bounded variation on any finite interval. Directly in terms of the characteristics of the Lévy canonical representation one can calculated the infinitesimal operator corresponding to the process  , regarded as a Markov random function. Many analytical properties of an infinitely-divisible distribution function can be expressed directly in terms of the characteristics of its Lévy canonical representation.
, regarded as a Markov random function. Many analytical properties of an infinitely-divisible distribution function can be expressed directly in terms of the characteristics of its Lévy canonical representation.
There are analogues of the Lévy canonical representation for infinitely-divisible distributions given on a wide class of algebraic structures.
References
| [1] | B.V. Gnedenko, A.N. Kolmogorov, "Limit distributions for sums of independent random variables" , Addison-Wesley (1954) (Translated from Russian) |
| [2] | V.V. Petrov, "Sums of independent random variables" , Springer (1975) (Translated from Russian) |
| [3] | Yu.V. [Yu.V. Prokhorov] Prohorov, Yu.A. Rozanov, "Probability theory, basic concepts. Limit theorems, random processes" , Springer (1969) (Translated from Russian) |
| [4] | I.I. [I.I. Gikhman] Gihman, A.V. [A.V. Skorokhod] Skorohod, "The theory of stochastic processes" , 2 , Springer (1975) (Translated from Russian) |
| [5] | K. Itô, "Stochastic processes" , Aarhus Univ. (1969) |
Comments
References
| [a1] | M. Loève, "Probability theory" , 1 , Springer (1977) |
| [a2] | L.P. Breiman, "Probability" , Addison-Wesley (1968) |
| [a3] | E. Lukacs, "Characteristic functions" , Griffin (1970) |
| [a4] | H. Heyer, "Probability measures on locally compact groups" , Springer (1977) |
| [a5] | K.R. Parthasarathy, "Probability measures on metric spaces" , Acad. Press (1967) |
| [a6] | B.V. Gnedenko, A.N. Kolmogorov, "Introduction to the theory of random processes" , Saunders (1969) (Translated from Russian) |
Lévy canonical representation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=L%C3%A9vy_canonical_representation&oldid=12582