Kruskal-Katona theorem
Let  and
and 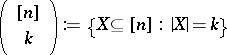 ,
, 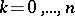 (cf. also Sperner property; Sperner theorem). The elements of
(cf. also Sperner property; Sperner theorem). The elements of 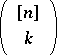 can be linearly ordered in the following way:
can be linearly ordered in the following way: 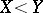 if the largest element in which
if the largest element in which 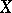 and
and 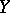 differ is in
differ is in 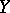 (cf. also Totally ordered set). If
(cf. also Totally ordered set). If 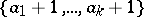 ,
, 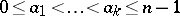 , is the
, is the 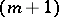 th element in this order, then
th element in this order, then
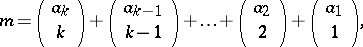 | (a1) |
since 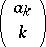
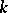 -element subsets of
-element subsets of 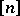 have maximal element smaller than
have maximal element smaller than 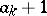 ,
, 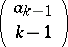 have maximal element
have maximal element 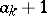 but the second largest element smaller than
but the second largest element smaller than 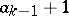 , etc.. Equation (a1) is called the
, etc.. Equation (a1) is called the 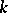 -representation of
-representation of 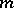 ,
, 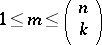 (for
(for 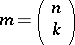 , one takes
, one takes 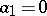 ,
, 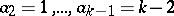 ,
,  ). This (unique) representation can be found directly by choosing
). This (unique) representation can be found directly by choosing 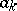 maximal such that
maximal such that 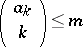 ,
, 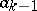 maximal such that
maximal such that 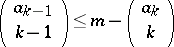 , etc..
, etc..
For a family 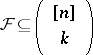 , the lower shadow of
, the lower shadow of 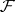 is defined by
is defined by
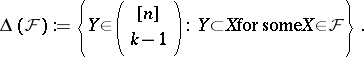 |
If 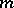 is given as above, then the lower shadow of the family of the first
is given as above, then the lower shadow of the family of the first 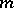 elements in
elements in 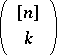 is the family of all
is the family of all 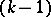 -element subsets of
-element subsets of 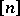 having maximal element smaller than
having maximal element smaller than 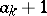 , of all
, of all 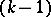 -element subsets of
-element subsets of 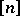 having maximal element
having maximal element 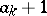 , but the second largest element smaller than
, but the second largest element smaller than 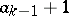 , etc., i.e. the family of the first
, etc., i.e. the family of the first 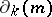 elements of
elements of 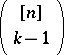 where
where
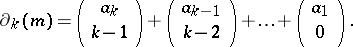 |
The Kruskal–Katona theorem states that in this way one obtains a lower shadow of minimum size, i.e., if  is any
is any 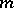 -element family in
-element family in 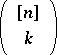 and
and 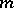 is given by (a1), then
is given by (a1), then
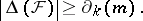 |
There exist generalizations to similar results for other partially ordered sets, like products of chains, products of stars, the partially ordered set of subwords of  -
- -words, and the partially ordered set of submatrices of a matrix.
-words, and the partially ordered set of submatrices of a matrix.
The following result of L. Lovász is weaker but numerically easier to handle: If 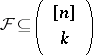 and
and 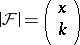 with some real
with some real  , where
, where 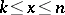 , then
, then
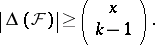 |
The original papers by J.B. Kruskal and G.O.H. Katona are [a3], [a4].
According to [a2], p. 1296, the Kruskal–Katona theorem is probably the most important one in finite extremal set theory.
References
| [a1] | K. Engel, "Sperner theory" , Cambridge Univ. Press (1997) |
| [a2] | P. Frankl, "Extremal set systems" R.L. Graham (ed.) M. Grötschel (ed.) L. Lovász (ed.) , Handbook of Combinatorics , 2 , Elsevier (1995) pp. 1293–1329 |
| [a3] | J.B. Kruskal, "The number of simplices in a complex" , Mathematical Optimization Techniques , Univ. California Press (1963) pp. 251–278 |
| [a4] | G.O.H. Katona, "A theorem of finite sets" , Theory of Graphs. Proc. Colloq. Tihany , Akad. Kiadó (1966) pp. 187–207 |
Kruskal-Katona theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kruskal-Katona_theorem&oldid=15000