Krull ring
Krull domain
A commutative integral domain  with the following property: There exists a family
with the following property: There exists a family  of discrete valuations on the field of fractions (cf. Fractions, ring of)
of discrete valuations on the field of fractions (cf. Fractions, ring of)  of
of  such that: a) for any
such that: a) for any  and all
and all  , except possibly a finite number of them,
, except possibly a finite number of them,  ; and b) for any
; and b) for any  ,
,  if and only if
if and only if  for all
for all 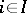 . Under these conditions,
. Under these conditions,  is said to be an essential valuation.
is said to be an essential valuation.
Krull rings were first studied by W. Krull [1], who called them rings of finite discrete principal order. They are the most natural class of rings in which there is a divisor theory (see also Divisorial ideal; Divisor class group). The ordered group of divisors of a Krull ring is canonically isomorphic to the ordered group  . The essential valuations of a Krull ring may be identified with the set of prime ideals of height 1. A Krull ring is completely integrally closed. Any integrally-closed Noetherian integral domain, in particular a Dedekind ring, is a Krull ring. The ring
. The essential valuations of a Krull ring may be identified with the set of prime ideals of height 1. A Krull ring is completely integrally closed. Any integrally-closed Noetherian integral domain, in particular a Dedekind ring, is a Krull ring. The ring 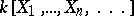 of polynomials in infinitely many variables is an example of a Krull ring which is not Noetherian. In general, any factorial ring is a Krull ring. A Krull ring is a factorial ring if and only if every prime ideal of height 1 is principal.
of polynomials in infinitely many variables is an example of a Krull ring which is not Noetherian. In general, any factorial ring is a Krull ring. A Krull ring is a factorial ring if and only if every prime ideal of height 1 is principal.
The class of Krull rings is closed under localization, passage to the ring of polynomials or formal power series, and also under integral closure in a finite extension of the field of fractions 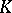 .
.
References
| [1] | W. Krull, "Allgemeine Bewertungstheorie" J. Reine Angew. Math. , 167 (1931) pp. 160–196 |
| [2] | O. Zariski, P. Samuel, "Commutative algebra" , 2 , Springer (1975) |
| [3] | N. Bourbaki, "Elements of mathematics. Commutative algebra" , Addison-Wesley (1972) (Translated from French) |
Comments
References
| [a1] | R.M. Fossum, "The divisor class group of a Krull domain" , Springer (1973) |
Krull ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Krull_ring&oldid=17884