Krull-Remak-Schmidt theorem
A series of propositions concerning the relationship between direct decompositions of a group or a ring. The lattice-theoretical version of the result is known as Ore's theorem (see Modular lattice). For a group  with an arbitrary system of operators, one has the following theorem of Schmidt (R. Remak proved the result for finite groups [2], and W. Krull — for rings [1]): If
with an arbitrary system of operators, one has the following theorem of Schmidt (R. Remak proved the result for finite groups [2], and W. Krull — for rings [1]): If  admits a principal series, then any two decompositions of
admits a principal series, then any two decompositions of  as a direct product with indecomposable factors are centrally isomorphic, i.e. there is a one-to-one correspondence between the sets of factors of each of the decompositions, and, if
as a direct product with indecomposable factors are centrally isomorphic, i.e. there is a one-to-one correspondence between the sets of factors of each of the decompositions, and, if  and
and  are corresponding factors, there exists an isomorphism
are corresponding factors, there exists an isomorphism  such that, for each
such that, for each  ,
,  lies in the centre of
lies in the centre of  ([3], see also [4]). Schmidt's theorem, as a theorem for groups with operators is, in particular, valid for modules over any ring. However, a module
([3], see also [4]). Schmidt's theorem, as a theorem for groups with operators is, in particular, valid for modules over any ring. However, a module  is indecomposable if its endomorphism ring is local (see Local ring), and under certain restrictions (e.g. if
is indecomposable if its endomorphism ring is local (see Local ring), and under certain restrictions (e.g. if  is a module of finite length) the converse is also true. In this connection, the Krull–Remak–Schmidt theorem for modules may be formulated as follows: Two decompositions
is a module of finite length) the converse is also true. In this connection, the Krull–Remak–Schmidt theorem for modules may be formulated as follows: Two decompositions
 |
where the endomorphism rings of the modules 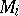 and
and  are local, are isomorphic. Moreover, each term in one of the decompositions may be replaced by some term of the other. In some cases this replacement may also be done for an infinite set of terms. A category-theoretic approach has been developed to investigate questions connected with the Krull–Remak–Schmidt theorem; it uses the category of submodules of direct sums of the modules in question.
are local, are isomorphic. Moreover, each term in one of the decompositions may be replaced by some term of the other. In some cases this replacement may also be done for an infinite set of terms. A category-theoretic approach has been developed to investigate questions connected with the Krull–Remak–Schmidt theorem; it uses the category of submodules of direct sums of the modules in question.
References
| [1] | W. Krull, "Algebraische Theorie der Ringe II" Math. Ann. , 91 (1924) pp. 1–46 |
| [2] | R. Remak, "Ueber die Zerlegung der endlichen Gruppen in direkte unzerlegbare Faktoren" J. Reine Angew. Math. , 139 (1911) pp. 293–308 |
| [3] | O.J. Schmidt, "Ueber unendliche Gruppen mit endlicher Kette" Math. Z. , 29 (1929) pp. 34–41 |
| [4] | A.G. Kurosh, "The theory of groups" , 1–2 , Chelsea (1955–1956) (Translated from Russian) |
| [5] | J. Lambek, "Lectures on rings and modules" , Blaisdell (1966) |
| [6] | C. Faith, "Algebra: rings, modules and categories" , 1–2 , Springer (1973–1976) |
| [7] | Itogi Nauk. i Tekhn. Algebra. Topol. Geom. , 14 (1976) pp. 57–190 |
Comments
Instead of Krull–Remak–Schmidt theorem one also finds Krull–Schmidt theorem.
The Euclidean decomposition theorem, so to speak, says that every natural number is a unique-up-to-permutation-of-the-factors product of prime powers. This fits into the present context by observing that if  , then
, then 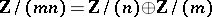 . The Lasker–Noether theorem generalizes this to state that in a commutative Noetherian ring with unit element every ideal is a finite irredundant intersection of primary ideals. Here an intersection of primary ideals
. The Lasker–Noether theorem generalizes this to state that in a commutative Noetherian ring with unit element every ideal is a finite irredundant intersection of primary ideals. Here an intersection of primary ideals 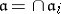 is irredundant if none of the
is irredundant if none of the  contains an intersection of the others and if the
contains an intersection of the others and if the  have distinct associated prime ideals
have distinct associated prime ideals  . The
. The  are then uniquely determined by
are then uniquely determined by  , [a1]. (Cf. also Lasker ring.)
, [a1]. (Cf. also Lasker ring.)
For an axiomatic approach to decomposition theories cf. [a2].
A natural setting for decomposition theories in Abelian categories are the so-called locally co-irreducible categories. Cf. [a3] for a discussion of these and their relation with Krull–Remak–Schmidt–Gabriel decomposition and tertiary decomposition for non-commutative Noetherian rings.
References
| [a1] | O. Zariski, P. Samuel, "Commutative algebra" , 1 , v. Nostrand (1958) pp. Chapt. IV, §4–5 |
| [a2] | J.A. Riley, "Axiomatic primary and tertiary decomposition theory" Trans. Amer. Math. Soc. , 105 (1962) pp. 177–201 |
| [a3] | N. Popescu, "Abelian categories with applications to rings and modules" , Acad. Press (1973) pp. Chapt. V |
Krull-Remak-Schmidt theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Krull-Remak-Schmidt_theorem&oldid=12042