Korovkin theorems
Korovkin's first theorem states that if  is an arbitrary sequence of positive linear operators on the space
is an arbitrary sequence of positive linear operators on the space  of real-valued continuous functions on the interval
of real-valued continuous functions on the interval  (cf. Continuous functions, space of; Linear operator) and if
(cf. Continuous functions, space of; Linear operator) and if
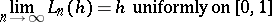 |
for all  , where
, where  (
( ,
,  ), then
), then
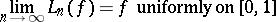 |
for all  .
.
The statement of Korovkin's second theorem is similar to that of the first theorem, but  is replaced by
is replaced by  (the space of
(the space of  -periodic real-valued functions on
-periodic real-valued functions on 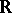 , endowed with the topology of uniform convergence on
, endowed with the topology of uniform convergence on 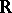 ) and
) and  is taken from the set
is taken from the set 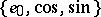 .
.
These theorems were proved by P.P. Korovkin in 1953 ([a3], [a4]). In 1952, H. Bohman [a2] had proved a result similar to Korovkin's first theorem but concerning sequences of positive linear operators on  of the form
of the form
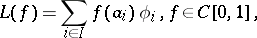 |
where 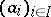 is a finite set of numbers in
is a finite set of numbers in  and
and 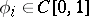 (
( ). Therefore Korovkin's first theorem is also known as the Bohman–Korovkin theorem. However, T. Popoviciu [a5] had already proved the essence of the theorem in 1950.
). Therefore Korovkin's first theorem is also known as the Bohman–Korovkin theorem. However, T. Popoviciu [a5] had already proved the essence of the theorem in 1950.
Korovkin has tried to generalize his first theorem by replacing  with other finite subsets of
with other finite subsets of  . He has shown that if a subset
. He has shown that if a subset  "behaves like"
"behaves like"  , then
, then  (Korovkin's third theorem). Moreover, he showed that a subset
(Korovkin's third theorem). Moreover, he showed that a subset 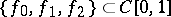 "behaves like"
"behaves like"  if and only if it is a Chebyshev system of order two.
if and only if it is a Chebyshev system of order two.
The Korovkin theorems are simple yet powerful tools for deciding whether a given sequence of positive linear operators on  or
or  is an approximation process. Furthermore, they have been the source of a considerable amount of research in several other fields of mathematics (cf. Korovkin-type approximation theory).
is an approximation process. Furthermore, they have been the source of a considerable amount of research in several other fields of mathematics (cf. Korovkin-type approximation theory).
See [a1] for a modern and comprehensive exposition of these results and for (some) applications.
References
| [a1] | F. Altomare, M. Campiti, "Korovkin-type approximation theory and its application" , de Gruyter studies in math. , 17 , de Gruyter (1994) |
| [a2] | H. Bohman, "On approximation of continuous and analytic functions" Ark. Math. , 2 (1952–1954) pp. 43–56 |
| [a3] | P.P. Korovkin, "On convergence of linear positive operators in the space of continuous functions" Dokl. Akad. Nauk. SSSR (N.S.) , 90 (1953) pp. 961–964 (In Russian) |
| [a4] | P.P. Korovkin, "Linear operators and approximation theory" , Gordon&Breach (1960) (In Russian) |
| [a5] | T. Popoviciu, "On the proof of the Weierstrass theorem using interpolation polynomials" Lucr. Ses. Gen. Stiintific. , 2 : 12 (1950) pp. 1664–1667 |
Korovkin theorems. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Korovkin_theorems&oldid=13016