Kolmogorov test
2020 Mathematics Subject Classification: Primary: 62G10 [MSN][ZBL]
A statistical test used for testing a simple non-parametric hypothesis $ H _ {0} $, according to which independent identically-distributed random variables $ X _ {1} \dots X _ {n} $ have a given distribution function $ F $, where the alternative hypothesis $ H _ {1} $ is taken to be two-sided:
$$ | {\mathsf E} F _ {n} ( x) - F ( x) | > 0 , $$
where $ {\mathsf E} F _ {n} $ is the mathematical expectation of the empirical distribution function $ F _ {n} $. The critical set of the Kolmogorov test is expressed by the inequality
$$ D _ {n} = \ \sup _ {| x | < \infty } \ | F _ {n} ( x) - F ( x) | > \lambda _ {n} $$
and is based on the following theorem, proved by A.N. Kolmogorov in 1933: If the hypothesis $ H _ {0} $ is true, then the distribution of the statistic $ D _ {n} $ does not depend on $ F $; also, as $ n \rightarrow \infty $,
$$ {\mathsf P} \{ \sqrt n D _ {n} < \lambda \} \rightarrow K ( \lambda ) ,\ \ \lambda > 0 , $$
where
$$ K ( \lambda ) = \ \sum _ {m = - \infty } ^ \infty ( - 1 ) ^ {m} e ^ {- 2 m ^ {2} \lambda ^ {2} } . $$
In 1948 N.V. Smirnov [BS] tabulated the Kolmogorov distribution function $ K ( \lambda ) $. According to the Kolmogorov test with significance level $ \alpha $, $ 0 < \alpha < 0.5 $, the hypothesis $ H _ {0} $ must be rejected if $ D _ {n} \geq \lambda _ {n} ( \alpha ) $, where $ \lambda _ {n} ( \alpha ) $ is the critical value of the Kolmogorov test corresponding to the given significance level $ \alpha $ and is the root of the equation $ {\mathsf P} \{ D _ {n} \geq \lambda \} = \alpha $.
To determine $ \lambda _ {n} ( \alpha ) $ one recommends the use of the approximation of the limiting law of the Kolmogorov statistic $ D _ {n} $ and its limiting distribution; see [B], where it is shown that, as $ n \rightarrow \infty $ and $ 0 < \lambda _ {0} < \lambda = O ( n ^ {1/3} ) $,
$$ \tag{* } {\mathsf P} \left \{ \frac{1}{18n} ( 6 n D _ {n} + 1 ) ^ {2} \geq \lambda \right \} = $$
$$ = \ \left [ 1 - K \left ( \sqrt { \frac \lambda {2} } \right ) \right ] \left [ 1 + O \left ( \frac{1}{n} \right ) \right ] . $$
The application of the approximation (*) gives the following approximation of the critical value:
$$ \lambda _ {n} ( \alpha ) \approx \ \sqrt { \frac{z}{2n} } - \frac{1}{6n} , $$
where $ z $ is the root of the equation $ 1 - K ( \sqrt {z/2 } ) = \alpha $.
In practice, for the calculation of the value of the statistic $ D _ {n} $ one uses the fact that
$$ D _ {n} = \ \max ( D _ {n} ^ {+} , D _ {n} ^ {-} ) , $$
where
$$ D _ {n} ^ {+} = \ \max _ {1 \leq m \leq n } \ \left ( \frac{m}{n} - F ( X _ {(} m) ) \right ) , $$
$$ D _ {n} ^ {-} = \max _ {1 \leq m \leq n } \left ( F ( X _ {(} m) ) - m- \frac{1}{n} \right ) , $$
and $ X _ {(} 1) \leq \dots \leq X _ {(} n) $ is the variational series (or set of order statistics) constructed from the sample $ X _ {1} \dots X _ {n} $. The Kolmogorov test has the following geometric interpretation (see Fig.).
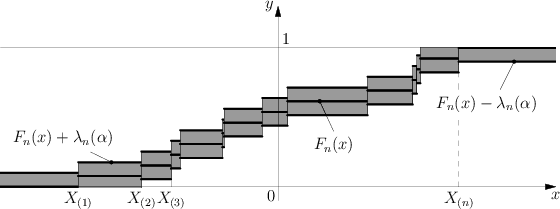
The graph of the functions $ F _ {n} ( x) $, $ F _ {n} ( x) \pm \lambda _ {n} ( \alpha ) $ is depicted in the $ xy $- plane. The shaded region is the confidence zone at level $ 1 - \alpha $ for the distribution function $ F $, since if the hypothesis $ H _ {0} $ is true, then according to Kolmogorov's theorem
$$ {\mathsf P} \{ F _ {n} ( x) - \lambda _ {n} ( \alpha ) < F ( x) < F _ {n} ( x) + \lambda _ {n} ( \alpha ) \} \approx 1 - \alpha . $$
If the graph of $ F $ does not leave the shaded region then, according to the Kolmogorov test, $ H _ {0} $ must be accepted with significance level $ \alpha $; otherwise $ H _ {0} $ is rejected.
The Kolmogorov test gave a strong impetus to the development of mathematical statistics, being the start of much research on new methods of statistical analysis lying at the foundations of non-parametric statistics.
References
| [K] | A.N. Kolmogorov, "Sulla determinizione empirica di una legge di distribuzione" Giorn. Ist. Ital. Attuari , 4 (1933) pp. 83–91 |
| [S] | N.V. Smirnov, "On estimating the discrepancy between empirical distribiution curves for two independent samples" Byull. Moskov. Gos. Univ. Ser. A , 2 : 2 (1938) pp. 3–14 (In Russian) |
| [B] | L.N. Bol'shev, "Asymptotically Pearson transformations" Theor. Probab. Appl. , 8 (1963) pp. 121–146 Teor. Veroyatnost. i Primenen. , 8 : 2 (1963) pp. 129–155 Zbl 0125.09103 |
| [BS] | L.N. Bol'shev, N.V. Smirnov, "Tables of mathematical statistics" , Libr. math. tables , 46 , Nauka (1983) (In Russian) (Processed by L.S. Bark and E.S. Kedrova) Zbl 0529.62099 |
Comments
Tests based on $ D _ {n} $ and $ \widetilde{D} _ {n} = \sup _ {x} ( F _ {n} ( x) - F ( x)) $, and similar tests for a two-sample problem based on $ D _ {m,n} = \sup _ {x} | F _ {m} ( x) - G _ {n} ( x) | $ and $ \widetilde{D} _ {m,n} = \sup _ {x} ( F _ {m} ( x) - G _ {n} ( x)) $, where $ G _ {m} $ is the empirical distribution function for samples of size $ m $ for a population with distribution function $ G $, are also called Kolmogorov–Smirnov tests, cf. also Kolmogorov–Smirnov test.
References
| [N] | G.E. Noether, "A brief survey of nonparametric statistics" R.V. Hogg (ed.) , Studies in statistics , Math. Assoc. Amer. (1978) pp. 3–65 Zbl 0413.62023 |
| [HW] | M. Hollander, D.A. Wolfe, "Nonparametric statistical methods" , Wiley (1973) MR0353556 Zbl 0277.62030 |
Kolmogorov test. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kolmogorov_test&oldid=47517