Kolmogorov duality
A duality in algebraic topology consisting in the isomorphism
 |
between the  -dimensional homology group
-dimensional homology group 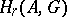 of a closed set
of a closed set 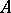 in a locally compact Hausdorff space
in a locally compact Hausdorff space 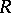 with zero
with zero  - and
- and 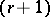 -dimensional homology groups, and the
-dimensional homology groups, and the  -dimensional homology group of the complement
-dimensional homology group of the complement 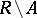 , with Abelian coefficient group
, with Abelian coefficient group 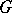 , as well as the isomorphism
, as well as the isomorphism
 |
between the corresponding cohomology groups, with  and
and  .
.
The homology and cohomology groups involved in these isomorphisms are defined as follows. An  -dimensional chain is taken to be any function
-dimensional chain is taken to be any function 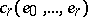 of
of  subsets of the space
subsets of the space 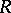 having compact closures that is skew-symmetric and additive in each of its arguments, takes values in
having compact closures that is skew-symmetric and additive in each of its arguments, takes values in 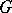 , and is equal to zero when the intersection
, and is equal to zero when the intersection  is empty. The boundary operator
is empty. The boundary operator 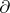 is defined by the formula
is defined by the formula
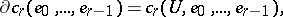 |
where 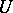 is any open subset of
is any open subset of  with compact closure containing
with compact closure containing 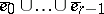 . The cycles are the chains
. The cycles are the chains  with zero boundaries,
with zero boundaries, 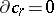 , and the cycles homologous to zero are the chains
, and the cycles homologous to zero are the chains 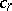 that are boundaries,
that are boundaries, 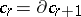 . The group
. The group 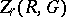 of all
of all  -dimensional cycles with the usual addition of functions contains the group
-dimensional cycles with the usual addition of functions contains the group 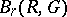 of all
of all  -dimensional boundaries as a subgroup. The quotient group
-dimensional boundaries as a subgroup. The quotient group 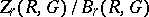 is the group
is the group  . A.N. Kolmogorov always considered the group
. A.N. Kolmogorov always considered the group  to be compact, and compactly topologized the homology group as well. However, the topology of the coefficient group has no effect on the structure of the homology group, and the homology can be taken over any group.
to be compact, and compactly topologized the homology group as well. However, the topology of the coefficient group has no effect on the structure of the homology group, and the homology can be taken over any group.
For the definition of cochains one considers the skew-symmetric functions 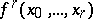 of
of  points
points  of the space
of the space 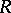 with values in
with values in 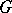 such that there exists for each
such that there exists for each 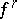 a finite system
a finite system 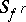 of pairwise-disjoint subsets of
of pairwise-disjoint subsets of 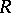 with compact closures and satisfying the condition
with compact closures and satisfying the condition 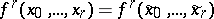 if
if  and
and  belong to the same element of the system
belong to the same element of the system 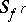 for any
for any 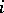 ;
;  if at least one of the
if at least one of the 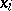 is not contained in any element of
is not contained in any element of 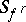 . The coboundary operator
. The coboundary operator 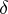 is defined by the formula
is defined by the formula
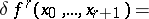 |
 |
Two functions 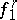 and
and 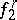 are regarded as equivalent if each point in
are regarded as equivalent if each point in  has a neighbourhood
has a neighbourhood 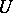 such that
such that  whenever all the
whenever all the 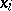 belong to
belong to 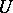 , and a cochain is taken to be an equivalence class of functions. The boundary of a cochain is defined as the class of coboundaries entering into this cochain of functions. A cocycle is a cochain
, and a cochain is taken to be an equivalence class of functions. The boundary of a cochain is defined as the class of coboundaries entering into this cochain of functions. A cocycle is a cochain 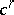 with zero coboundary and a cocycle is cohomologous to zero if it is a coboundary,
with zero coboundary and a cocycle is cohomologous to zero if it is a coboundary, 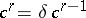 . The group
. The group  of all
of all  -dimensional coboundaries is a subgroup of the group
-dimensional coboundaries is a subgroup of the group  of all
of all  -dimensional cocycles; the quotient group
-dimensional cocycles; the quotient group 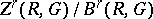 then defines the group
then defines the group  .
.
The homology and cohomology groups defined in this way, which is often referred to as the functional way, were introduced by Kolmogorov . He then went on to prove that, apart from the indicated duality isomorphism, there is a duality between the homology and cohomology groups 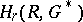 and
and 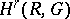 in the sense of the Pontryagin theory of characters, when the compact group
in the sense of the Pontryagin theory of characters, when the compact group  is dual to the group
is dual to the group 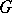 , and the Poincaré duality
, and the Poincaré duality
 |
where 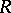 is an open
is an open  -dimensional manifold,
-dimensional manifold, 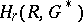 and
and 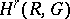 are functional groups over a compact (or discrete) group
are functional groups over a compact (or discrete) group 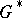 (or
(or 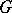 ), and
), and 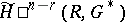 and
and 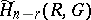 are the cohomology (homology) groups of infinite cochains (finite chains) of an arbitrary cellular decomposition of
are the cohomology (homology) groups of infinite cochains (finite chains) of an arbitrary cellular decomposition of 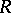 .
.
In the case when 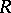 is the
is the  -dimensional Euclidean space, one obtains from the above dualities the Pontryagin duality theorem (see Alexander duality). A special case of these dualities is the Steenrod duality theorem (see Duality in algebraic topology), since the Kolmogorov duality for homology is valid also for arbitrary coefficient groups [2].
-dimensional Euclidean space, one obtains from the above dualities the Pontryagin duality theorem (see Alexander duality). A special case of these dualities is the Steenrod duality theorem (see Duality in algebraic topology), since the Kolmogorov duality for homology is valid also for arbitrary coefficient groups [2].
The functional homology groups are isomorphic: to the Vietoris groups (see Vietoris homology) in the case of compact metric spaces and compact coefficient groups ; to the Aleksandrov spectral homology groups with respect to singular subcomplexes [3] in the case of locally compact spaces and compact coefficient groups [4] and, consequently, to the Aleksandrov–Čech homology groups of the one-point compactification of a given locally compact space [5]; and to the Steenrod homology groups [8] in the case of compact metric spaces and arbitrary groups [7]. Thus, the Kolmogorov homology groups introduced four years earlier than those of Steenrod are a generalization of the latter to a wider class of spaces.
The functional homology and cohomology groups satisfy all the Steenrod–Eilenberg axioms on the category of locally compact spaces with admissible mappings (that is, when the pre-image of each compact set is compact) [6] and in addition the two Milnor axioms on the category of compact metric spaces [7].
References
| [1a] | A.N. Kolmogorov, "Les groupes de Betti des espaces localement bicompacts" C.R. Acad. Sci. , 202 (1936) pp. 1144–1147 |
| [1b] | A.N. Kolmogorov, "Propriétés des groupes de Betti des espaces localement bicompacts" C.R. Acad. Sci. , 202 (1936) pp. 1325–1327 |
| [1c] | A.N. Kolmogorov, "Les groupes de Betti des espaces métriques" C.R. Acad. Sci. , 202 (1936) pp. 1558–1560 |
| [1d] | A.N. Kolmogorov, "Cycles rélatifs. Théorème de dualité de M. Alexander" C.R. Acad. Sci. , 202 (1936) pp. 1641–1643 |
| [2] | L.D. Mdzinarishvili, "On Kolmogorov's duality law" Soviet Math. Dokl. , 15 (1974) pp. 840–843 Dokl. Akad. Nauk SSSR , 216 : 3 (1974) pp. 502–504 |
| [3] | P.S. Aleksandrov, "General theory of homology" Uchen. Zap. Moscov. Gos. Univ. , 45 (1940) pp. 3–60 (In Russian) |
| [4] | G.S. Chogoshvili, "On the equivalence of functional and spectral homology theory" Izv. Akad. Nauk SSSR. Ser. Mat. , 15 : 5 (1951) pp. 421–438 (In Russian) |
| [5] | N.E. Steenrod, S. Eilenberg, "Foundations of algebraic topology" , Princeton Univ. Press (1966) |
| [6] | M.B. Balavadze, "On Kolmogorov's duality theory" Trudy Tbilisi Mat. Inst. , 41 (1972) pp. 5–40 (In Russian) |
| [7] | L.D. Mdzinarishvili, "The equivalence of Kolmogorov's and Steenrod's homology theories" Trudy Tbilisi Mat. Inst. , 41 (1972) pp. 143–163 (In Russian) (French and Georgian summaries) |
| [8] | N. Steenrod, "Regular cycles of compact metric spaces" Ann. of Math. , 41 (1940) pp. 833–851 |
Comments
The homology and cohomology groups defined above are also known as the Kolmogorov–Alexander, or Alexander–Kolmogorov, homology groups (, [a1]) and the Kolmogorov–Spanier cohomology groups (, [a2]).
References
| [a1] | J.W. Alexander, "On the chains of a complex and their duals" Proc. Nat. Acad. Sci. USA , 21 (1935) pp. 509–512 |
| [a2] | E.H. Spanier, "Cohomology theory for general spaces" Ann. of Math. , 49 (1948) pp. 407–427 |
| [a3] | J.W. Milnor, "On axiomatic homology theory" Pacific J. Math. , 12 (1962) pp. 337–341 |
Kolmogorov duality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kolmogorov_duality&oldid=18080