Kolmogorov-Smirnov test
2020 Mathematics Subject Classification: Primary: 62G10 [MSN][ZBL]
A non-parametric test used for testing a hypothesis 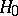 , according to which independent random variables
, according to which independent random variables 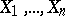 have a given continuous distribution function
have a given continuous distribution function 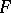 , against the one-sided alternative
, against the one-sided alternative 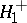 :
: 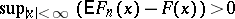 , where
, where 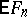 is the mathematical expectation of the empirical distribution function
is the mathematical expectation of the empirical distribution function 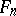 . The Kolmogorov–Smirnov test is constructed from the statistic
. The Kolmogorov–Smirnov test is constructed from the statistic
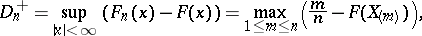 |
where 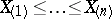 is the variational series (or set of order statistics) obtained from the sample
is the variational series (or set of order statistics) obtained from the sample 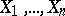 . Thus, the Kolmogorov–Smirnov test is a variant of the Kolmogorov test for testing the hypothesis
. Thus, the Kolmogorov–Smirnov test is a variant of the Kolmogorov test for testing the hypothesis  against a one-sided alternative
against a one-sided alternative 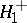 . By studying the distribution of the statistic
. By studying the distribution of the statistic 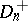 , N.V. Smirnov [1] showed that
, N.V. Smirnov [1] showed that
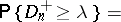 | (1) |
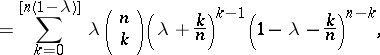 |
where 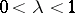 and
and 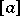 is the integer part of the number
is the integer part of the number  . Smirnov obtained in addition to the exact distribution (1) of
. Smirnov obtained in addition to the exact distribution (1) of 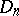 its limit distribution, namely: If
its limit distribution, namely: If 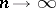 and
and 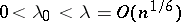 , then
, then
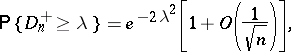 |
where 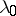 is any positive number. By means of the technique of asymptotic Pearson transformation it has been proved [2] that if
is any positive number. By means of the technique of asymptotic Pearson transformation it has been proved [2] that if 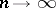 and
and  , then
, then
 | (2) |
According to the Kolmogorov–Smirnov test, the hypothesis 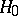 must be rejected with significance level
must be rejected with significance level 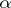 whenever
whenever
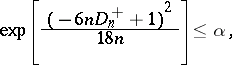 |
where, by virtue of (2),
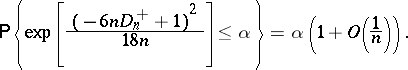 |
The testing of  against the alternative
against the alternative 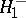 :
: 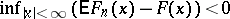 is dealt with similarly. In this case the statistic of the Kolmogorov–Smirnov test is the random variable
is dealt with similarly. In this case the statistic of the Kolmogorov–Smirnov test is the random variable
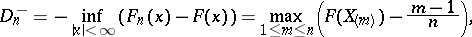 |
whose distribution is the same as that of the statistic 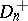 when
when 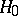 is true.
is true.
References
| [1] | N.V. Smirnov, "Approximate distribution laws for random variables, constructed from empirical data" Uspekhi Mat. Nauk , 10 (1944) pp. 179–206 (In Russian) |
| [2] | L.N. Bol'shev, "Asymptotically Pearson transformations" Theor. Probab. Appl. , 8 (1963) pp. 121–146 Teor. Veroyatnost. i Primenen. , 8 : 2 (1963) pp. 129–155 |
| [3] | L.N. Bol'shev, N.V. Smirnov, "Tables of mathematical statistics" , Libr. math. tables , 46 , Nauka (1983) (In Russian) (Processed by L.S. Bark and E.S. Kedrova) |
| [4] | B.L. van der Waerden, "Mathematische Statistik" , Springer (1957) |
Comments
There is also a two-sample Kolmogorov–Smirnov test, cf. the editorial comments to Kolmogorov test and, for details, [a1], [a2].
References
| [a1] | G.E. Noether, "A brief survey of nonparametric statistics" R.V. Hogg (ed.) , Studies in statistics , Math. Assoc. Amer. (1978) pp. 39–65 |
| [a2] | M. Hollander, D.A. Wolfe, "Nonparametric statistical methods" , Wiley (1973) |
Kolmogorov-Smirnov test. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kolmogorov-Smirnov_test&oldid=21350