Kolmogorov-Chapman equation

An equation of the form

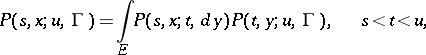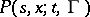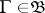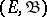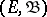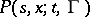that is, a condition imposed on the transition function (, , , being a measurable space), enabling one (under certain conditions on ) to construct a Markov process for which the conditional probability is the same as . Conversely, for a Markov process its transition function 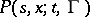, which by definition is equal to 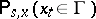, satisfies the Kolmogorov–Chapman equation, as follows immediately from general properties of conditional probabilities. This was pointed out by S. Chapman [1] and investigated by A.N. Kolmogorov in 1931 (see [2]).

References

[1]	S. Chapman, Proc. Roy. Soc. Ser. A , 119 (1928) pp. 34–54
[2]	A. [A.N. Kolmogorov] Kolmogoroff, "Ueber die analytischen Methoden in der Wahrscheinlichkeitsrechnung" Math. Ann. , 104 (1931) pp. 415–458
[3]	I.I. [I.I. Gikhman] Gihman, A.V. [A.V. Skorokhod] Skorohod, "The theory of stochastic processes" , 2 , Springer (1975) (Translated from Russian)

Comments

In Western literature this equation is usually referred to as the Chapman–Kolmogorov equation.

See also (the editorial comments to) Einstein–Smoluchowski equation.

References

[a1]	P. Lévy, "Processus stochastiques et mouvement Brownien" , Gauthier-Villars (1965)
[a2]	E.B. Dynkin, "Markov processes" , 1 , Springer (1965) pp. Sect. 5.26 (Translated from Russian)
[a3]	W. Feller, "An introduction to probability theory and its applications" , 1 , Wiley (1966) pp. Chapt. XV.13