Koebe function
From Encyclopedia of Mathematics
The function
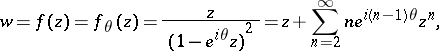 |
where 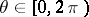 . This function was first studied by P. Koebe [1]. The Koebe function maps the disc
. This function was first studied by P. Koebe [1]. The Koebe function maps the disc  onto the
onto the 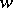 -plane with a slit along the ray starting at the point
-plane with a slit along the ray starting at the point 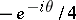 , its extension containing the point
, its extension containing the point 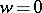 . The Koebe function is an extremal function in a number of problems in the theory of univalent functions (cf. Bieberbach conjecture; Univalent function).
. The Koebe function is an extremal function in a number of problems in the theory of univalent functions (cf. Bieberbach conjecture; Univalent function).
References
| [1] | P. Koebe, "Ueber die Uniformisierung beliebiger analytischen Kurven" Math. Ann. , 69 (1910) pp. 1–81 |
| [2] | W.K. Hayman, "Coefficient problems for univalent functions and related function classes" J. London Math. Soc. , 40 : 3 (1965) pp. 385–406 |
| [3] | G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian) |
How to Cite This Entry:
Koebe function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Koebe_function&oldid=19034
Koebe function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Koebe_function&oldid=19034
This article was adapted from an original article by E.G. Goluzina (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article