Knapsack problem

Given a knapsack (container) of total capacity , and objects with weights and respective values , the problem is to pack as much value in the knapsack as possible.

Abstractly the problem can be formulated as follows. Given positive integers , , , the problem is to maximize subject to and .

The greedy algorithm to "solve" this proceeds as follows. It is natural to favour objects with the greatest value/weight density. So, relabel, if needed, the objects so that . Then select recursively according to

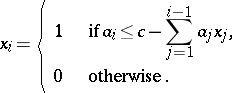This greedy algorithm has a performance ratio of , i.e. it is guaranteed to find a solution which is within a factor of the optimal one.

If the are allowed to take fractional values (i.e. values in instead of 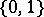), then the greedy algorithm is optimal.

The knapsack problem is 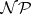-hard, cf. .

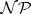References

[a1]	"Encyclopedia of Operations Research and Management Science" S.I. Gass (ed.) C.M. Harris (ed.) , Kluwer Acad. Publ. (1996) pp. 325–326
[a2]	M. Grötschel, L. Lovász, "Combinatorial optimization" R.L. Graham (ed.) M. Grötschel (ed.) L. Lovász (ed.) , Handbook of Combinatorics , Elsevier (1995) pp. 1541–1579