Klein surface
Klein bottle
A closed one-sided surface of genus 1 (see Fig. a, a, b).

Figure: k055510a
The Klein surface can be obtained from a square  (see Fig. b) by identifying the points of the line segments
(see Fig. b) by identifying the points of the line segments  and
and  lying on the lines parallel to the side
lying on the lines parallel to the side  and the points of the segments
and the points of the segments  and
and  symmetric with respect to the centre of the square
symmetric with respect to the centre of the square  .
.

Figure: k055510b
The Klein surface can be topologically imbedded in the  -dimensional Euclidean space, but not in
-dimensional Euclidean space, but not in  -dimensional space.
-dimensional space.
Attention was drawn to the Klein surface by F. Klein (1874).
Comments
A Klein bottle can be obtained by glueing together two crosscaps (Möbius bands, cf. Möbius strip) along their boundaries. The homology of the Klein bottle 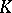 is:
is:  ,
, 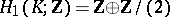 ,
, 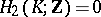 . Its Euler characteristic is
. Its Euler characteristic is 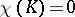 . Together with the torus it is the only smooth
. Together with the torus it is the only smooth  -dimensional surface which admits deformations of the identity mapping that have no fixed points.
-dimensional surface which admits deformations of the identity mapping that have no fixed points.
References
| [a1] | D.W. Blackett, "Elementary topology" , Acad. Press (1967) |
| [a2] | K. Jänich, "Topology" , Springer (1984) (Translated from German) |
| [a3] | J. Mayer, "Algebraic topology" , Prentice-Hall (1972) |
Klein surface. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Klein_surface&oldid=16791