Kirchhoff formula
Kirchhoff integral
The formula
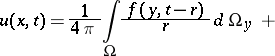 | (1) |
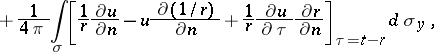 |
expressing the value 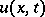 of the solution of the inhomogeneous wave equation
of the solution of the inhomogeneous wave equation
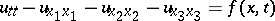 | (2) |
at the point 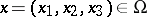 at the instant of time
at the instant of time 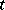 in terms of the retarded volume potential
in terms of the retarded volume potential
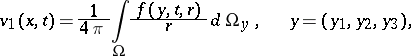 |
with density 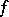 , and in terms of the values of the function
, and in terms of the values of the function 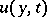 and its first-order derivatives on the boundary
and its first-order derivatives on the boundary 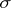 of the domain
of the domain  at the instant of time
at the instant of time 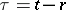 . Here
. Here  is a bounded domain in the three-dimensional Euclidean space with a piecewise-smooth boundary
is a bounded domain in the three-dimensional Euclidean space with a piecewise-smooth boundary 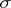 ,
,  is the outward normal to
is the outward normal to 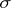 and
and 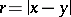 is the distance between
is the distance between  and
and 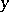 .
.
Let
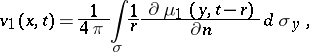 |
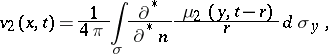 |
where
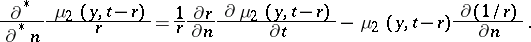 |
The integrals 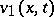 and
and  are called the retarded potentials of the single and the double layer.
are called the retarded potentials of the single and the double layer.
The Kirchhoff formula (1) means that any twice continuously-differentiable solution 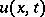 of equation (2) can be expressed as the sum of the retarded potentials of a single layer, a double layer and a volume potential:
of equation (2) can be expressed as the sum of the retarded potentials of a single layer, a double layer and a volume potential:
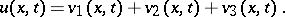 |
In the case when 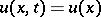 and
and 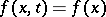 do not depend on
do not depend on 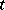 , the Kirchhoff formula takes the form
, the Kirchhoff formula takes the form
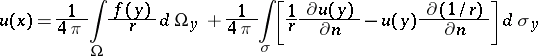 |
and gives a solution of the Poisson equation 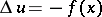 .
.
The Kirchhoff formula is widely applied in the solution of a whole series of problems. For example, if  is the ball
is the ball 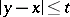 of radius
of radius 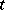 and centre
and centre  , then formula (1) is transformed into the relation
, then formula (1) is transformed into the relation
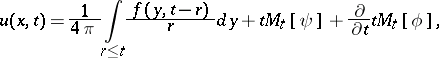 | (3) |
where
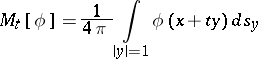 |
is the average value of 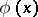 over the surface of the sphere
over the surface of the sphere 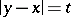 ,
,
 | (4) |
If 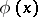 and
and 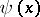 are given functions in the ball
are given functions in the ball 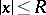 , with continuous partial derivatives of orders three and two, respectively, and
, with continuous partial derivatives of orders three and two, respectively, and 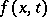 is a twice continuously-differentiable function for
is a twice continuously-differentiable function for 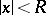 ,
,  , then the function
, then the function 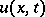 defined by (3) is a regular solution of the Cauchy problem (4) for equation (2) when
defined by (3) is a regular solution of the Cauchy problem (4) for equation (2) when 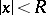 and
and 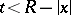 .
.
Formula (3) is also called Kirchhoff's formula.
The Kirchhoff formula in the form
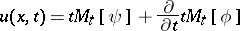 |
for the wave equation
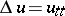 | (5) |
is remarkable in that the Huygens principle does follow from it: The solution (wave)  of (5) at the point
of (5) at the point 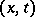 of the space of independent variables
of the space of independent variables 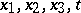 is completely determined by the values of
is completely determined by the values of 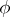 ,
, 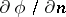 and
and 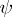 on the sphere
on the sphere 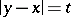 with centre at
with centre at  and radius
and radius 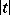 .
.
Consider the following equation of normal hyperbolic type:
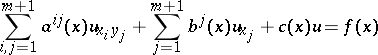 | (6) |
with sufficiently-smooth coefficients 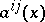 ,
, 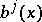 ,
, 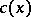 , and right-hand side
, and right-hand side 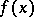 in some
in some 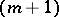 -dimensional domain
-dimensional domain 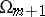 , that is, a form
, that is, a form
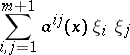 |
that at any point 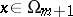 can be reduced by means of a non-singular linear transformation to the form
can be reduced by means of a non-singular linear transformation to the form
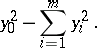 |
The Kirchhoff formula generalizes to equation (6) in the case when the number 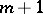 of independent variables
of independent variables 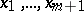 is even [4]. Here the essential point is the construction of the function
is even [4]. Here the essential point is the construction of the function 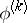 that generalizes the Newton potential
that generalizes the Newton potential 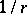 to the case of equation (6). For the special case of equation (6),
to the case of equation (6). For the special case of equation (6),
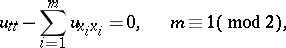 | (7) |
the generalized Kirchhoff formula is
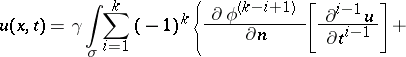 | (8) |
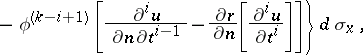 |
where 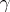 is a positive number,
is a positive number,  is the piecewise-smooth boundary of an
is the piecewise-smooth boundary of an  -dimensional bounded domain
-dimensional bounded domain 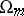 containing the point
containing the point 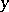 in its interior, and
in its interior, and  is the outward normal to
is the outward normal to 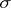 . Further,
. Further,
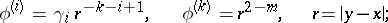 |
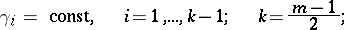 |
and 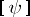 denotes the retarded value of
denotes the retarded value of 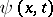 :
:
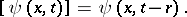 |
Formula (8) for equation (6) is sometimes called the Kirchhoff–Sobolev formula.
References
| [1] | A.V. Bitsadze, "Equations of mathematical physics" , MIR (1980) (Translated from Russian) |
| [2] | V.S. Vladimirov, "Equations of mathematical physics" , MIR (1984) (Translated from Russian) |
| [3] | H. Bateman, "Partial differential equations of mathematical physics" , Dover (1944) |
| [4] | M. Mathisson, "Eine neue Lösungsmethode für Differentialgleichungen von normalem hyperbolischem Typus" Math. Ann. , 107 (1932) pp. 400–419 |
| [5] | M. Mathisson, "Le problème de M. Hadamard rélatifs à la diffusion des ondes" Acta Math. , 71 : 3–4 (1939) pp. 249–282 |
| [6] | S.G. Mikhlin, "Linear partial differential equations" , Moscow (1977) (In Russian) |
| [7] | S.L. Sobolev, "Sur une généralisation de la formule de Kirchhoff" Dokl. Akad. Nauk SSSR , 1 : 6 (1933) pp. 256–262 |
| [8] | S.L. Sobolev, "Applications of functional analysis in mathematical physics" , Amer. Math. Soc. (1963) (Translated from Russian) |
| [9] | V.I. Smirnov, "A course of higher mathematics" , 4 , Addison-Wesley (1964) (Translated from Russian) |
| [10] | A.N. [A.N. Tikhonov] Tichonoff, A.A. Samarskii, "Differentialgleichungen der mathematischen Physik" , Deutsch. Verlag Wissenschaft. (1959) (Translated from Russian) |
Comments
References
| [a1] | B.B. Baker, E.T. Copson, "The mathematical theory of Huygens's principle" , Clarendon Press (1950) |
| [a2] | L. Schwartz, "Théorie des distributions" , 2 , Hermann (1951) |
| [a3] | G.R. Kirchhoff, "Vorlesungen über mathematischen Physik" Ann. der Physik , 18 (1883) |
Kirchhoff formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kirchhoff_formula&oldid=14522