Kharitonov polynomial theory
A theory concerned with the root locations for a family of polynomials (cf. Polynomial). A good general reference for this area is [a1]. The motivation for this theory derives from the issue of robust stability for systems of linear time-invariant differential equations. For a system of linear differential equations (cf. Differential equation, ordinary)
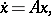 |
stability is determined by the roots of the characteristic polynomial
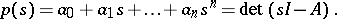 |
The system of differential equations will be stable if and only if all roots of this characteristic polynomial lie in the open left half of the complex plane. In this case, the polynomial  is said to be Hurwitz stable. For a single polynomial, the question of stability can be determined using the Routh–Hurwitz criterion.
is said to be Hurwitz stable. For a single polynomial, the question of stability can be determined using the Routh–Hurwitz criterion.
The question of robust stability arises when it is supposed that the system of differential equations depends on uncertain parameters whose values are unknown but satisfy known bounds. The presence of such uncertain parameters means that the coefficients of the characteristic polynomial are unknown but bounded. This then defines a family of characteristic polynomials. The system will be robustly stable if all polynomials in this family have all their roots in the open left half of the complex plane.
The most important result in this area is a theorem due to V.L. Kharitonov [a2]. In this result, the polynomial family considered is a collection of polynomials with the following specific form:
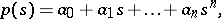 |
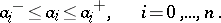 |
Thus, each coefficient of the polynomial is contained within a given interval. Such a polynomial family is referred to as an interval polynomial. Kharitonov's theorem gives a necessary and sufficient condition for the robust stability of such an interval polynomial in terms of the following four polynomials:
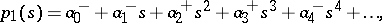 |
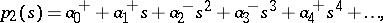 |
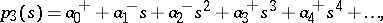 |
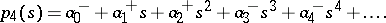 |
The interval polynomial is robustly stable if and only if these four polynomials are Hurwitz stable.
One of the main limitations of Kharitonov's theorem is the restriction that the polynomial family must have the structure of an interval polynomial. An important result which applies to a much more general class of polynomial families is the edge theorem, [a3]. This theorem applies to a polynomial family consisting of a collection of polynomials of the form:
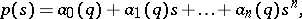 |
where
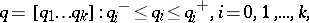 |
and where the functions 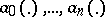 are affine linear. In such a polynomial family, the polynomial coefficients are contained in a polytope. The edge theorem states that the polynomial family will be robustly stable if and only if for each exposed edge of this polytope, the corresponding one-dimensional polynomial family is robustly stable.
are affine linear. In such a polynomial family, the polynomial coefficients are contained in a polytope. The edge theorem states that the polynomial family will be robustly stable if and only if for each exposed edge of this polytope, the corresponding one-dimensional polynomial family is robustly stable.
References
| [a1] | B.R. Barmish, "New tools for robustness of linear systems" , Macmillan (1994) |
| [a2] | V.L. Kharitonov, "Asymptotic stability of an equilibrium position of a family of systems of linear differential equations" Differentsial'nye Uraveniya , 14 (1978) pp. 2086–2088 (In Russian) |
| [a3] | A.C. Bartlett, C.V. Hollot, L. Huang, "Root locations of an entire polytope of polynomials: It suffices to check the edges" Math. Control, Signals and Systems , 1 (1988) pp. 61–71 |
Kharitonov polynomial theory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kharitonov_polynomial_theory&oldid=19085