Kernel pair
of a morphism in a category
A categorical generalization of the equivalence relation induced by a mapping of one set into another. A pair of morphisms 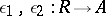 in a category
in a category 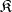 is called a kernel pair of the morphism
is called a kernel pair of the morphism 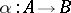 if
if  , and if for any pair of morphisms
, and if for any pair of morphisms 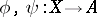 for which
for which 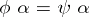 there is a unique morphism
there is a unique morphism 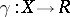 such that
such that 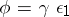 and
and 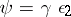 .
.
Let 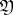 be an arbitrary category of universal algebras of a given type and all homomorphisms between them that is closed with respect to finite products, and let
be an arbitrary category of universal algebras of a given type and all homomorphisms between them that is closed with respect to finite products, and let 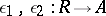 be a kernel pair of a homomorphism
be a kernel pair of a homomorphism 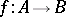 in
in 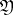 . Then the image of the homomorphism
. Then the image of the homomorphism
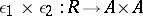 |
induced by the pair 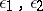 is a congruence on the algebra
is a congruence on the algebra 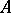 (cf. also Congruence (in algebra)). Conversely, if
(cf. also Congruence (in algebra)). Conversely, if 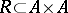 is an arbitrary congruence on
is an arbitrary congruence on 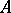 ,
, 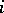 is the imbedding of
is the imbedding of 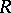 into
into 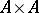 , and
, and 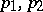 are the projections of
are the projections of 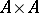 onto
onto 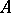 , then the pair of homomorphisms
, then the pair of homomorphisms 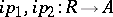 is a kernel pair of the natural homomorphism of
is a kernel pair of the natural homomorphism of 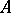 onto the quotient algebra
onto the quotient algebra 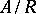 .
.
In an arbitrary category with finite products and kernels of pairs of morphisms (cf. Kernel of a morphism in a category), the kernel pair of a morphism 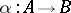 is constructed as follows. One chooses a product
is constructed as follows. One chooses a product 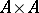 with the projections
with the projections 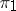 and
and 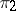 , and determines the kernel
, and determines the kernel 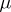 of the pair of morphisms
of the pair of morphisms 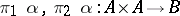 . Then the pair of morphisms
. Then the pair of morphisms 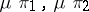 is a kernel pair of
is a kernel pair of 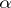 .
.
Comments
A cokernel pair is defined dually.
References
| [a1] | F.G. Manes, "Algebraic categories" , Springer (1976) pp. Chapt. 2, §1 |
| [a2] | H. Schubert, "Kategorien" , 2 , Springer (1970) pp. Sect. 18.4 |
| [a3] | S. MacLane, "Categories for the working mathematician" , Springer (1971) pp. Sects. 3.3, 3.4 |
Kernel pair. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kernel_pair&oldid=17146