Kernel of an integral operator
From Encyclopedia of Mathematics
A function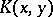 
in two variables that defines an integral operator 
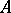by the equality
 |
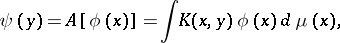where 
ranges over a measure space 
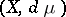and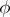 
belongs to a certain space of functions defined on 
.
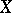Comments
References
| [a1] | I.C. Gohberg, S. Goldberg, "Basic operator theory" , Birkhäuser (1981) |
| [a2] | P.R. Halmos, V.S. Sunder, "Bounded integral operators on 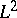 spaces" , Springer (1978) |
| [a3] | K. Jörgens, "Lineare Integraloperatoren" , Teubner (1970) |
| [a4] | V.I. Smirnov, "A course of higher mathematics" , 4 , Addison-Wesley (1964) (Translated from Russian) |
| [a5] | P.P. Zabreiko (ed.) A.I. Koshelev (ed.) M.A. Krasnoselskii (ed.) S.G. Mikhlin (ed.) L.S. Rakovshchik (ed.) V.Ya. Stet'senko (ed.) T.O. Shaposhnikova (ed.) R.S. Anderssen (ed.) , Integral equations - a reference text , Noordhoff (1975) (Translated from Russian) |
How to Cite This Entry:
Kernel of an integral operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kernel_of_an_integral_operator&oldid=16737
Kernel of an integral operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kernel_of_an_integral_operator&oldid=16737
This article was adapted from an original article by G.L. Litvinov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article