Kernel congruence
From Encyclopedia of Mathematics
of a homomorphism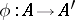 
of algebraic systems
The congruence (cf. Congruence (in algebra))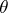 
on 
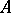consisting of all pairs 
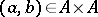for which 
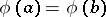. For any congruence 
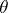on an algebraic system there is a homomorphism 
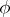of this system for which 
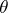is the kernel congruence. If 
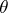is the kernel congruence of a strong homomorphism 
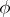of an algebraic system 
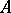onto a system 
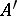, then the canonical mapping 
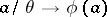, where 
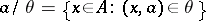, is an isomorphism of the quotient system 
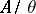onto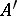 
.
For references see Homomorphism.
How to Cite This Entry:
Kernel congruence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kernel_congruence&oldid=11822
Kernel congruence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kernel_congruence&oldid=11822
This article was adapted from an original article by D.M. Smirnov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article